
分析 由已知条件利用相互独立事件概率乘法公式列出方程组,能求出P(B)的值.
解答 解:∵事件A,B,C相互独立,P(A•B)=$\frac{1}{6}$,P($\overline{B}$•C)=$\frac{1}{8}$,P(A•B•$\overline{C}$)=$\frac{1}{8}$,
∴$\left\{\begin{array}{l}{P(A)P(B)=\frac{1}{6}}\\{(1-P(B))P(C)=\frac{1}{8}}\\{P(A)P(B)(1-P(C))=\frac{1}{8}}\end{array}\right.$,解得P(C)=$\frac{1}{4}$,P(B)=$\frac{1}{2}$,P(A)=$\frac{1}{3}$.
∴P(B)=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意相互独立事件概率乘法公式的合理运用.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2$\sqrt{2}$)∪(2$\sqrt{5}$,+∞) | B. | (2$\sqrt{2}$,3$\sqrt{2}$] | C. | (3$\sqrt{2}$,2$\sqrt{5}$] | D. | [2$\sqrt{2}$,2$\sqrt{5}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不论采取哪种抽样方法,这100个零件中每个被抽到的概率都是$\frac{1}{5}$ | |
| B. | ①②两种抽样方法,这100个零件中每个被抽到的概率都是$\frac{1}{5}$,③并非如此 | |
| C. | ①③两种抽样方法,这100个零件中每个被抽到的概率都是$\frac{1}{5}$,②并非如此 | |
| D. | 采用不同的抽样方法,这100个零件中每个被抽到的概率各不相同 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
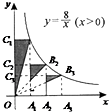 如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=$\frac{8}{x}({x>0})$的图象分别交于点B1、B2、B3,分别过点B1,B2,B3作x轴的平行线,分别与y轴交于点C1,C2,C3,连接OB1,OB2,OB3,那么图中阴影部分的面积之和为$\frac{49}{9}$.
如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=$\frac{8}{x}({x>0})$的图象分别交于点B1、B2、B3,分别过点B1,B2,B3作x轴的平行线,分别与y轴交于点C1,C2,C3,连接OB1,OB2,OB3,那么图中阴影部分的面积之和为$\frac{49}{9}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com