
分析 (1)an+1-an>0,解得k<$\frac{2n+1}{2}$,进而证明.
(2)$?n∈{N^*},\frac{a_n}{n}≥1$,可得$n+\frac{6}{n}$≥2k+1,利用数列的单调性即可得出.
解答 (1)证明:an+1-an=(n+1)2-2k(n+1)+6-[n2-2kn+6]=2n+1-2k>0,解得k<$\frac{2n+1}{2}$,
∴k<$\frac{3}{2}$.
∴k≤1是{an}为递增数列的充分不必要条件;
(2)解:∵$?n∈{N^*},\frac{a_n}{n}≥1$,
∴$n+\frac{6}{n}$-2k≥1,即$n+\frac{6}{n}$≥2k+1,
∵$n+\frac{6}{n}$≥5,
∴2k+1≤5,
∴k≤2.
∴k的取值范围是k≤2.
点评 本题考查了数列的单调性、充要条件的判定、恒成立问题,考查了推理能力与计算能力,属于中档题.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,0) | C. | $(-∞,-\frac{1}{5})$ | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
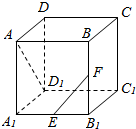 长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=a,E和F分别是A1B1和BB1的中点,求:
长方体ABCD-A1B1C1D1中,AB=BC=2a,AA1=a,E和F分别是A1B1和BB1的中点,求:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{3}{2}$,0] | B. | [0,$\frac{3}{2}$] | C. | [-1,0] | D. | [-$\frac{3}{2}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
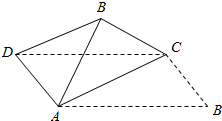 如图,将矩形纸片ABCD(其中$AB=\sqrt{3}$,BC=1)沿对角线AC折起后,使得异面直线BC⊥AD,则此时异面直线AB和CD所成的角的余弦值是( )
如图,将矩形纸片ABCD(其中$AB=\sqrt{3}$,BC=1)沿对角线AC折起后,使得异面直线BC⊥AD,则此时异面直线AB和CD所成的角的余弦值是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com