
分析 (1)直接利用函数奇偶性的定义判断求解即可;
(2)利用单调增函数的定义判断证明即可.
解答 解:(1)函数$f(x)=x-\frac{1}{x}$,
的定义域为(-∞,0)∪(0,+∞),$f(-x)=-x-\frac{1}{-x}=-(x-\frac{1}{x})=-f(x)$
即f(-x)=-f(x),所以f(x)是奇函数.(4分)
(2)证明:x1,x2∈(0,+∞),x1<x2,有$f({x_2})-f({x_1})={x_2}-\frac{1}{x_2}-({x_1}-\frac{1}{x_1})=\frac{{({x_2}-{x_1})(1+{x_1}{x_2})}}{{{x_1}{x_2}}}$,
∵$0<{x_1}<{x_2}⇒\left\{\begin{array}{l}{x_2}-{x_1}>0\\ 1+{x_1}{x_2}>0\\{x_1}{x_2}>0\end{array}\right.⇒f({x_2})-f({x_1})>0$,
∴函数f(x)在(0,+∞)上是增函数.(8分)
点评 本题考查函数的奇偶性以及单调性的判断与证明,是基本知识的考查.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{5}$ | B. | $-\frac{1}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
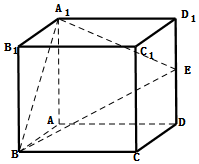 如图,在正方体ABCD-A1B1C1D1中,棱长为a,E是棱DD1的中点
如图,在正方体ABCD-A1B1C1D1中,棱长为a,E是棱DD1的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=log22x | B. | y=$\sqrt{{x}^{2}}$ | C. | y=2${\;}^{lo{g}_{2}x}$ | D. | y=($\sqrt{x}$)2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com