
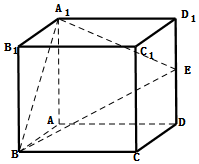
 如图,在正方体ABCD-A1B1C1D1中,棱长为a,E是棱DD1的中点
如图,在正方体ABCD-A1B1C1D1中,棱长为a,E是棱DD1的中点分析 (1)代入棱锥的体积公式计算;
(2)取C1D1中点F,连B1F,EF,C1D,连B1A交A1B于O,则可证四边形B1OEF为平行四边形,得出BF∥OE,从而得出B1F∥平面A1BE.
解答 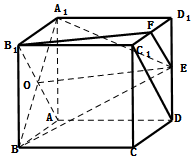 解:(1)${V_{E-{A_1}{B_1}B}}=\frac{1}{3}{S_{△{A_1}{B_1}B}}h=\frac{a^3}{6}$.
解:(1)${V_{E-{A_1}{B_1}B}}=\frac{1}{3}{S_{△{A_1}{B_1}B}}h=\frac{a^3}{6}$.
(2)存在.
取C1D1中点F,连B1F,EF,C1D,连B1A交A1B于O,
∵EF是△D1C1D的中位线∴$EF∥CD,EH=\frac{1}{2}{C_1}D$,
因为正方体ABCD-A1B1C1D1
所以${B_1}O=\frac{1}{2}{B_1}A$
又因为四边形B1ADC1是平行四边形,
所以B1A∥C1D,B1A=C1D
所以B1O∥EF,B1O=EF,
所以四边形B1OEF是平行四边形,
所以B1F∥OE,
所以B1F∥平面A1BE.
点评 本题考查了线面平行的判定,棱锥的体积计算,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,+∞) | C. | ($\frac{1}{3}$,1) | D. | (3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45 | B. | -45 | C. | 1335 | D. | -1335 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com