
分析 先根据向量的数量积的运算,求出A=60°,再建立坐标系,得到$\overrightarrow{PA}$•$\overrightarrow{PB}$=x(x-4)+3=x2-4x+3=(x-2)2-1,构造函数f(x),利用函数的单调性求出函数的值域m,问题得以解决.
解答 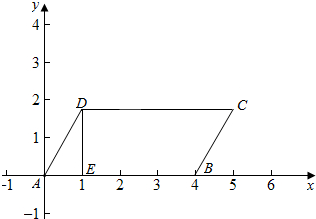 解:∵平行四边形ABCD中,AB=4,AD=2,$\overrightarrow{AB}$•$\overrightarrow{AD}=4$,点P在边CD上,
解:∵平行四边形ABCD中,AB=4,AD=2,$\overrightarrow{AB}$•$\overrightarrow{AD}=4$,点P在边CD上,
∴|$\overrightarrow{AB}$|•|$\overrightarrow{AD}$|•cos∠A=4,∴cosA=$\frac{1}{2}$,∴A=60°,
以A为原点,以AB所在的直线为x轴,以AB的垂线为y轴,
建立如图所示的坐标系,∴A(0,0),B(4,0),D(1,$\sqrt{3}$),
设P(x,$\sqrt{3}$),则1≤x≤5,∴$\overrightarrow{PA}$=(-x,-$\sqrt{3}$),$\overrightarrow{PB}$=(4-x,-$\sqrt{3}$),
∴$\overrightarrow{PA}$•$\overrightarrow{PB}$=x(x-4)+3=x2-4x+3=(x-2)2-1,
设f(x)=(x-2)2-1,则f(x)在[1,2)上单调递减,在[2,5]上单调递增,
∴f(x)min=f(2)=-1,f(x)max=f(5)=8,
∴$\overrightarrow{PA}$•$\overrightarrow{PB}$ 的取值范围是[-1,8],则$\overrightarrow{PA}$•$\overrightarrow{PB}$的最大值是8,
故答案为:8.
点评 本题考查了向量的数量积运算和向量的坐标的数量积和函数的最值问题,关键是建立坐标系,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{5}$ | B. | $-\frac{1}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
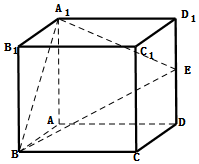 如图,在正方体ABCD-A1B1C1D1中,棱长为a,E是棱DD1的中点
如图,在正方体ABCD-A1B1C1D1中,棱长为a,E是棱DD1的中点查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com