
 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.分析 (1)取PD中点F,连接AF,EF,可得四边形ABEF是平行四边形,即可的BE∥AF,BE∥面PAD;
(2)可得PA⊥DC.CD⊥面PAD,即AF⊥DC,且AF∥BE,得BE⊥CD;
(3)点E为棱PC的中点,PA⊥底面ABCD,${V_{P-BDE}}={V_{B-PDE}}=\frac{1}{2}{V_{B-PDC}}=\frac{1}{2}{V_{P-BDC}}=\frac{1}{6}{S_{△BDC}}.PA=\frac{2}{3}$.
解答 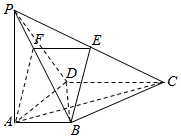 证明:(1)取PD中点F,连接AF,EF,
证明:(1)取PD中点F,连接AF,EF,
∵E,F分别是PC,PD的中点,
∴$EF∥CD,EF=\frac{1}{2}CD$∵$AB∥CD,AB=\frac{1}{2}CD$,
∴EF∥AB,EF=AB∴四边形ABEF是平行四边形,
∴BE∥AF,又BE?面PAD,AF?面PAD∴BE∥面PAD,
(2 由PA⊥面ABCD,DC?面ABCD,∴PA⊥DC.
$\begin{array}{l}又∵AD⊥DC$,∴$DC⊥面PAD\\∴DC⊥AF$,∴AF⊥DC,且AF∥BE,
∴BE⊥CD;
(3)∵点E为棱PC的中点,PA⊥底面ABCD,
∴${V_{P-BDE}}={V_{B-PDE}}=\frac{1}{2}{V_{B-PDC}}=\frac{1}{2}{V_{P-BDC}}=\frac{1}{6}{S_{△BDC}}.PA=\frac{2}{3}$.
点评 本题考查了空间线面平行、线线垂直的判定,考查了等体积法求体积,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 16 | C. | 26 | D. | 27 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE,且AE=1,AB=2.
如图,正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE,且AE=1,AB=2. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若$\vec a•\vec b=\vec b•\vec c$,则$\vec a=\vec c$ | B. | 与向量$\vec a$共线的单位向量为$±\frac{\vec a}{{|{\vec a}|}}$ | ||
| C. | 若$\vec a∥\vec b$,$\vec b∥\vec c$,则$\vec a∥\vec c$ | D. | 若$\vec a∥\vec b$,则存在唯一实数λ使得$\vec a=λ\vec b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com