
已知等差数列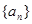 的公差不为零,其前n项和为
的公差不为零,其前n项和为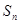 ,若
,若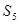 =70,且
=70,且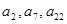 成等比数列,
成等比数列,
(1)求数列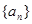 的通项公式;
的通项公式;
(2)设数列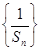 的前n项和为
的前n项和为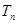 ,求证:
,求证: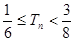 .
.
(1) ;(2)答案详见解析.
;(2)答案详见解析.
解析试题分析:数列问题要注意以下两点①等差(比)数列中各有5个基本量,建立方程组可“知三求二”;②数列的本质是定义域为正整数集或其有限子集的函数,数列的通项公式即为相应的解析式,因此在解决数列问题时,应注意用函数的思想求解.(1)由题知,展开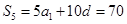 ,又
,又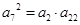 ,利用等差数列通项公式展开,得
,利用等差数列通项公式展开,得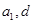 方程,联立求
方程,联立求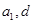 ,进而求数列
,进而求数列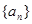 的通项公式;(2)求数列前
的通项公式;(2)求数列前 项和,首先考虑其通项公式
项和,首先考虑其通项公式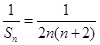 ,利用裂项相消法,求得
,利用裂项相消法,求得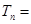
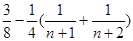 ,将其看作自变量为
,将其看作自变量为 的函数,求其值域即可.
的函数,求其值域即可.
试题解析:(1)由题知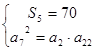 ,即
,即 , 2分
, 2分
解得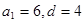 或
或 (舍去), 4分
(舍去), 4分
所以数列的通项公式为 . 4分
. 4分
(2)由(1)得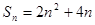 7分
7分
则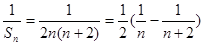 8分
8分
则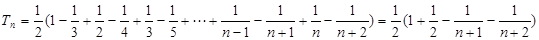
=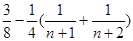 10分
10分
由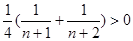 可知
可知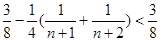 ,即
,即 11分
11分
由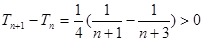 可知
可知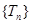 是递增数列,则
是递增数列,则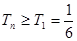 13分
13分
可证得: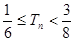 14分
14分
考点:1、等差数列的通项公式;2、等差数列前前 项和;3、裂项相消法.
项和;3、裂项相消法.


科目:高中数学 来源: 题型:解答题
从数列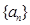 中抽出一些项,依原来的顺序组成的新数列叫数列
中抽出一些项,依原来的顺序组成的新数列叫数列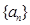 的一个子列.
的一个子列.
(1)写出数列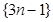 的一个是等比数列的子列;
的一个是等比数列的子列;
(2)设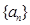 是无穷等比数列,首项
是无穷等比数列,首项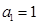 ,公比为
,公比为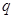 .求证:当
.求证:当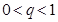 时,数列
时,数列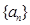 不存在
不存在
是无穷等差数列的子列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在数列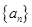 中,
中,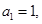 且对任意的
且对任意的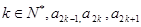 成等比数列,其公比为
成等比数列,其公比为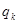 ,
,
(1)若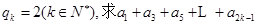 ;
;
(2)若对任意的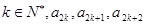 成等差数列,其公差为
成等差数列,其公差为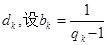 .
.
①求证: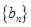 成等差数列,并指出其公差;
成等差数列,并指出其公差;
②若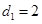 ,试求数列
,试求数列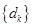 的前
的前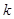 项和
项和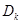 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
知{an}是首项为-2的等比数列,Sn是其前n项和,且S3,S2,S4成等差数列,
(1)求数列{an}的通项公式.
(2)若bn=log2|an|,求数列{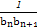 }的前n项和Tn.
}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知等差数列{an}是递增数列,且满足a4·a7=15,a3+a8=8.
(1)求数列{an}的通项公式;
(2)令bn= (n≥2),b1=
(n≥2),b1=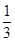 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com