Question

7．已知偶函数y=f（x）的定义域为R，且对任意实数x，恒有f（$\frac{1}{2}$+x）=f（$\frac{1}{2}$-x），当x∈[0，$\frac{1}{2}$]，f（x）=（x-$\frac{1}{2}$）²．
（1）求证：f（x）为周期函数；
（2）当x∈R时，求f（x）的解析式；
（3）解不等式f（sinx）＜f（cosx）．

Answer 1

分析 （1）根据函数周期性的定义即可证明f（x）为周期函数；
（2）先求出函数在一个周期内的解析式，然后根据函数周期性即可求出当x∈R时，求f（x）的解析式；
（3）作出函数在一个周期[-1，1]内的图象，判断函数的单调性，结合函数单调性和奇偶性的性质将不等式f（sinx）＜f（cosx）转化为f（|sinx|）＜f（|cosx|）进行求解即可．

解答 解：（1）∵y=f（x）是偶函数，且f（$\frac{1}{2}$+x）=f（$\frac{1}{2}$-x），
∴f（$\frac{1}{2}$+x）=f（$\frac{1}{2}$-x）=f（$\frac{1}{2}$+x）=-f（x-$\frac{1}{2}$），
即f（x+1）=-f（x），即f（x+2）=f（x），
则f（x）为周期为2的周期函数；
（2）若x∈[-$\frac{1}{2}$，0]，则-x∈[0，$\frac{1}{2}$]，
此时f（-x）=（x-$\frac{1}{2}$）²，
∵f（x）是偶函数，
∴f（-x）=（-x-$\frac{1}{2}$）²=f（x），
即f（x）=（-x-$\frac{1}{2}$）²=（x+$\frac{1}{2}$）²，x∈[-$\frac{1}{2}$，0]，
若x∈[$\frac{1}{2}$，1]，则-x∈[-1，-$\frac{1}{2}$]，
则1-x∈[0，$\frac{1}{2}$]，
∵f（x+1）=-f（x），
∴f（x）=-f（x-1）=-f（1-x）=-（1-x-$\frac{1}{2}$）²=-（x-$\frac{1}{2}$）²．x∈[$\frac{1}{2}$，1]，
若x∈[-1，-$\frac{1}{2}$]，则-x∈[$\frac{1}{2}$，1]，
则f（-x）=-（-x-$\frac{1}{2}$）²=f（x），
即f（x）=-（x+$\frac{1}{2}$）²．x∈[-1，-$\frac{1}{2}$]，
则当x∈R时，则f（x）的解析式为f（x）=$\left\{\begin{array}{l}{-（x+\frac{1}{2}）^{2}，}&{x∈[2k-1，2k-\frac{1}{2}]}\\{（x+\frac{1}{2}）^{2}，}&{x∈（2k-\frac{1}{2}，2k）}\\{（x-\frac{1}{2}）^{2}，}&{x∈[2k，2k+\frac{1}{2}]}\\{-（x-\frac{1}{2}）^{2}，}&{x∈（2k+\frac{1}{2}，2k+1]}\end{array}\right.$；
（3）作出函数f（x）在[-1，1]上的图象如图，
则函数在[0，1]上为减函数，
则不等式f（sinx）＜f（cosx）．
等价为f（|sinx|）＜f（|cosx|）．
即|sinx|＞|cosx|．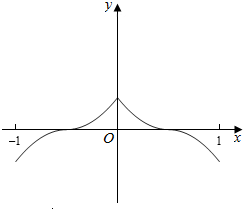
平方得sin²x＞cos²x，
即cos²x-sin²x＜0，
即cos2x＜0，
则2kπ+$\frac{π}{2}$＜2x＜2kπ+$\frac{3π}{2}$，
即kπ+$\frac{π}{4}$＜x＜kπ+$\frac{3π}{4}$，
即不等式的解集为（kπ+$\frac{π}{4}$，kπ+$\frac{3π}{4}$），k∈Z．

点评 本题主要考查函数解析式的求解，以及函数奇偶性和周期性的判断和应用，综合考查函数的性质，利用分类讨论和数形结合是解决本题的关键．综合性较强，有一定的难度．