
分析 利用椭圆$\frac{{x}^{2}}{64}$+$\frac{{y}^{2}}{36}$=1,可得a2=64,b2=36,即可得到a,b,c,进而得到长轴长、短轴长、顶点坐标、离心率.
解答 解:∵椭圆$\frac{{x}^{2}}{64}$+$\frac{{y}^{2}}{36}$=1,∴a2=64,b2=36.
∴a=8,b=6,c=2$\sqrt{7}$.
∴椭圆的长轴和短轴的长分别为2a=16,2b=12.
顶点(±8,0),(0,±6).
离心率e=$\frac{c}{a}$=$\frac{\sqrt{7}}{4}$.
点评 熟练掌握椭圆的标准方程及其性质是解题的关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (5x)'=5x | B. | (5x)'=5xln5 | C. | $({log_a}x)'=\frac{lna}{x}$ | D. | .$({log_a}x)'=\frac{a}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{7}{10}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
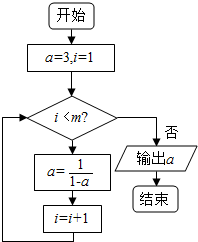
| A. | 3 | B. | -$\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com