练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知椭圆与抛物线有相同的焦点，为原点，点是抛物线准线上一动点，点在抛物线上，且，则的最小值为（    ）

    A．          B．        C．           D．


    A

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    ，均为等差数列，前项和分别为

        A．       B．       C．       D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     的定义域是

      A.     B．

      C.     D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图已知抛物线 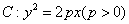的准线为 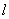，焦点为F，圆M的圆心在x轴的正半轴上，且与y轴相切，过原点作倾斜角为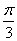的直线t，交 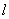于点A，交圆M于点B，且 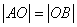=2.

    (I)求圆M和抛物线C的方程；

    (Ⅱ)已知点N(4，0)，设G，H是抛物线上异于原点O的两个不同点，且N，G，H三点共线，证明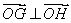： 并求△GOH面积的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是( )

    A． B． C． D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


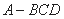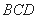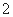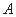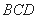    在三棱锥中，底面为边长为的正三角形，顶点在底面上的射

    影为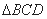的中心， 若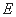为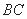的中点，且直线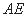与底面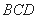所成角的正切值为

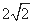    ，则三棱锥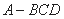外接球的表面积为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若集合，，则     ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某地农业监测部门统计发现：该地区近几年的生猪收购价格每四个月会重复出现，但生猪养殖成本逐月递增．下表是今年前四个月的统计情况：

    月份

    1月份

    2月份

    3月份

    4月份

    收购价格（元/斤）

    6

    7

    6

    5

    养殖成本（元/斤）

    3

    4

    4．6

    5

    现打算从以下两个函数模型：①，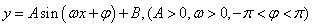

    ②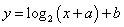中选择适当的函数模型，分别来拟合今年生猪收购价格（元/斤）与相应月份之间的函数关系、养殖成本（元/斤）与相应月份之间的函数关系．

    （1）请你选择适当的函数模型，分别求出这两个函数解析式；

    （2）按照你选定的函数模型，帮助该部门分析一下，今年该地区生猪养殖户在接下来的月份里有没有可能亏损?

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知递增的等比数列{an}满足a2＋a3＋a4＝28，且a3＋2是a2、a4的等差中项．

    (1)求数列{an}的通项公式；

    (2)若bn＝log2an＋1，Sn是数列{bn}的前n项和，求使Sn>42＋4n成立的n的最小值．

    查看答案和解析>>

    同步练习册答案