
【题目】如图,棱锥![]() 的地面
的地面![]() 是矩形,
是矩形, ![]() 平面
平面![]() ,
,![]() ,
,![]() .
.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先证明![]() 为正方形,可得
为正方形,可得![]() ,由
,由![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,可得
,可得![]() ,利用线面垂直的判定定理可得结果;(2)以
,利用线面垂直的判定定理可得结果;(2)以![]() 为
为![]() 轴建立空间直角坐标系,根据向量垂直数量积为零,列方程组求出平面
轴建立空间直角坐标系,根据向量垂直数量积为零,列方程组求出平面![]() 的法向量,结合
的法向量,结合![]() 为平面
为平面![]() 的法向量,利用空间向量夹角余弦公式求出两个向量的夹角余弦,进而转化为二面角
的法向量,利用空间向量夹角余弦公式求出两个向量的夹角余弦,进而转化为二面角![]() 的平面角即可;(3)求出平面
的平面角即可;(3)求出平面![]() 的法向量,再求出平面的斜线
的法向量,再求出平面的斜线![]() 所在的向量
所在的向量![]() ,然后求出
,然后求出![]() 在法向量上的射影即可得到点到平面的距离.
在法向量上的射影即可得到点到平面的距离.
(1)解法一:在![]() 中,
中, ![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() 为正方形,
为正方形,
因此![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() .又∵
.又∵![]() ,
,
∴![]() 平面
平面![]() .
.
解法二:以![]() 为
为![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中, ![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,
即![]() ,
,![]() .又
.又![]() ,
,
∴![]() 平面
平面![]() .
.

(2)解法一:由![]() 平面
平面![]() ,
,
知![]() 为
为![]() 在平面
在平面![]() 上的射影.
上的射影.
又![]() ,∴
,∴![]() ,
,
∴![]() 为二面角
为二面角![]() 的平面角.
的平面角.
又∵![]() ,∴
,∴![]() .
.
解法二:由1题得![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,
,![]() ,
,
即![]() ,∴
,∴![]() ,
,
故平面![]() 的法向量可取为
的法向量可取为![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() 为平面
为平面![]() 的法向量.
的法向量.
设二面角![]() 的大小为
的大小为![]() ,
,
依题意可得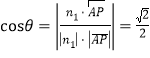 ,
,
∴![]() .
.
(3)解法一:∵![]() ,
,
∴![]() ,
,
设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
由![]() ,
,
有![]() ,
,
得![]() .
.
解法二:由1题得![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() ,
,![]() ,
,
即![]() ,
,
∴![]() .
.
故平面![]() 的法向量可取为
的法向量可取为![]() .
.
∵![]() ,
,
∴![]() 到平面
到平面![]() 的距离为
的距离为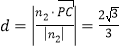 .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,D、E分别是△ABC的边BC的三等分点,设 ![]() =m,
=m, ![]() =n,∠BAC=
=n,∠BAC= ![]() .
. 
(1)用 ![]() 、
、 ![]() 分别表示
分别表示 ![]() ,
, ![]() ;
;
(2)若 ![]()
![]() =15,|
=15,| ![]() |=3
|=3 ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 上有最大值4 和最小值1,设
上有最大值4 和最小值1,设![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 在区间
在区间![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线x2=2py和 ![]() ﹣y2=1的公切线PQ(P是PQ与抛物线的切点,未必是PQ与双曲线的切点)与抛物线的准线交于Q,F(0,
﹣y2=1的公切线PQ(P是PQ与抛物线的切点,未必是PQ与双曲线的切点)与抛物线的准线交于Q,F(0, ![]() ),若
),若 ![]() |PQ|=
|PQ|= ![]() |PF|,则抛物线的方程是( )
|PF|,则抛物线的方程是( ) 
A.x2=4y
B.x2=2 ![]() y
y
C.x2=6y
D.x2=2 ![]() y
y
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某大型水上乐园内有一块矩形场地![]() 米,
米, ![]() 米,以
米,以![]() 为直径的半圆
为直径的半圆![]() 和半圆
和半圆![]() (半圆在矩形
(半圆在矩形![]() 内部)为两个半圆形水上主题乐园,
内部)为两个半圆形水上主题乐园, ![]() 都建有围墙,游客只能从线段
都建有围墙,游客只能从线段![]() 处进出该主题乐园.为了进一步提高经济效益,水上乐园管理部门决定沿着
处进出该主题乐园.为了进一步提高经济效益,水上乐园管理部门决定沿着![]() 修建不锈钢护栏,沿着线段
修建不锈钢护栏,沿着线段![]() 修建该主题乐园大门并设置检票口,其中
修建该主题乐园大门并设置检票口,其中![]() 分别为
分别为![]() 上的动点,
上的动点, ![]() ,且线段
,且线段![]() 与线段
与线段![]() 在圆心
在圆心![]() 和
和![]() 连线的同侧.已知弧线部分的修建费用为
连线的同侧.已知弧线部分的修建费用为![]() 元/米,直线部门的平均修建费用为
元/米,直线部门的平均修建费用为![]() 元/米.
元/米.

(1)若![]() 米,则检票等候区域(其中阴影部分)面积为多少平方米?
米,则检票等候区域(其中阴影部分)面积为多少平方米?
(2)试确定点![]() 的位置,使得修建费用最低.
的位置,使得修建费用最低.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网络营销和电子商务的兴起,人们的购物方式更具多样化,某调查机构随机抽取10名购物者进行采访,5名男性购物者中有3名倾向于选择网购,2名倾向于选择实体店,5名女性购物者中有2名倾向于选择网购,3名倾向于选择实体店.
(1)若从10名购物者中随机抽取2名,其中男、女各一名,求至少1名倾向于选择实体店的概率;
(2)若从这10名购物者中随机抽取3名,设X表示抽到倾向于选择网购的男性购物者的人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正△ABC三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点E是线段AB的中点,过点E作球O的截面,则截面面积的最小值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣4|,g(x)=|2x+1|.
(1)解不等式f(x)<g(x);
(2)若2f(x)+g(x)>ax对任意的实数x恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com