
分析 (Ⅰ)化圆的一般方程为标准方程,求出圆心坐标和半径,由圆心到直线的距离小于半径列式求得a值;
(Ⅱ)求出PC所在直线的斜率,得到AB所在直线的斜率,进一步得到AB方程,由点到直线的距离公式求出圆心C到直线AB的距离,代入三角形面积公式得答案.
解答 解:(Ⅰ)依题意可知:直线l:ax-y+5=0(a>0)
与圆C:x2+y2-2x-24=0,即(x-1)2+y2=25有两个不同交点,
则圆心C(1,0)到直线l的距离d<r(r表示圆C的半径),
于是有:$d=\frac{{|{a+5}|}}{{\sqrt{{a^2}+1}}}<r=5$⇒$|{a+5}|<5\sqrt{{a^2}+1}$,
不等式两边同时平方可得:(a+5)2<25(a2+1),
化简整理可得:12a2-5a>0(a>0),
解之得:$a>\frac{5}{12}$.
故所求实数a的取值范围是$a∈({\frac{5}{12},+∞})$;
(Ⅱ)由垂径定理知:弦AB的垂直平分线l′过圆心C(1,0),
又直线l过点P(-2,4),
故可得直线l′的斜率${k_{PC}}=\frac{4-0}{-2-1}=-\frac{4}{3}$,
而弦AB所在直线l斜率kAB满足kAB•kCP=-1,
于是可得:${k_{AB}}=-\frac{1}{{{k_{CP}}}}=\frac{3}{4}$,即有$a={k_{AP}}=\frac{3}{4}$,
从而弦AB所在直线l的方程为$\frac{3}{4}x-y+5=0$,即3x-4y+20=0,
由点到直线的距离公式可得:圆心C(1,0)到直线l的距离为$d=\frac{{|{3×1+20}|}}{{\sqrt{{3^2}+{4^2}}}}=\frac{23}{5}$,
根据垂径定理:${({\frac{1}{2}|{AB}|})^2}+{d^2}={r^2}$,
得:${|{AB}|^2}=4({{r^2}-{d^2}})=4[{25-{{({\frac{23}{5}})}^2}}]=\frac{384}{25}⇒|{AB}|=\frac{{8\sqrt{6}}}{5}$,
故三角形ABC的面积:${S_{△ABC}}=\frac{1}{2}|{AB}|d=\frac{1}{2}×\frac{{8\sqrt{6}}}{5}×\frac{23}{5}=\frac{92}{25}\sqrt{6}$.
点评 本题考查直线与圆的位置关系,着重考查垂径定理的应用,是中档题.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)=f′(1) | B. | f(1)>f′(1) | C. | f(1)<f′(1) | D. | 无法判断 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
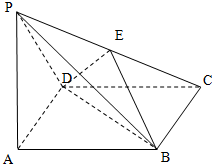 在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,PA=AB,E是PC的中点.
在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,PA=AB,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 都大于2 | B. | 都小于2 | ||
| C. | 至多有一个小于2 | D. | 至少有一个不小于2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com