
| A. | 32 | B. | 57 | C. | 75 | D. | 480 |
分析 题意得:在所有非空子集中每个元素出现2n-1次.故有2n-1个子集含1,有2n-2个子集不含1含2,有2n-3子集不含1,2,含3…有2i-1个子集不含1,2,3…i-1,而含i,进而利用错位相减法求出其和.
解答 解:由题意得:在所有非空子集中每个元素出现2n-1次.
故有2n-1个子集含1,有2n-2个子集不含1含2,有2n-3子集不含1,2,含3…有2i-1个子集不含1,2,3…i-1,而含i.
所以Sn=2n-1×1+2n-2×2+…+21×(n-1)+n
Sn=n•1+(n-1)•2+…+2•2n-2+1•2n-1…①
所以2Sn=n•2+(n-1)•4+…+2•2n-1+1•2n…②
所以①-②可得-Sn=n-(2+4+…+2n-1+2n)
所以Sn=2n+1-n-2
所以S5=26-5-2=57.
故选:B
点评 本题考查了错位相减法、等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 椭圆 | B. | 线段 | C. | 不存在 | D. | 椭圆或线段 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年级 | 高一 | 高二 | 高三 |
| 数量 | 50 | 150 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
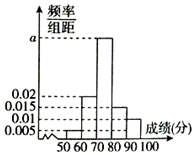 为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.
为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.| 男生 | 女生 | 合计 | |
| 优 秀 | |||
| 不优秀 | |||
| 合 计 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com