Question

17．在△ABC中，角A，B，C的对边分别为a，b，c，AH为边BC上的高，有以下结论：
①$\overrightarrow{AC}•\frac{{\overrightarrow{AH}}}{{|{\overrightarrow{AH}}|}}=c\;sinB$； 
②$\overrightarrow{BC}•（\overrightarrow{AC}-\overrightarrow{AB}）={b^2}+{c^2}-2bccosA$；
③$\overrightarrow{AH}•\overrightarrow{AC}={\overrightarrow{AH}^2}$；
④$\overrightarrow{AH}•（\overrightarrow{AB}+\overrightarrow{BC}）=\overrightarrow{AH}•\overrightarrow{AB}$．
其中所有的正确序号的是①②③④．

Answer 1

分析 利用平面向量的数量积定义，结合三角形中向量的线性运算法则对每一个命题进行分析、判断，即可得出结果．

解答 解：如图所示，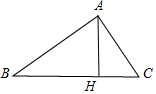
对于①，$\overrightarrow{AC}$•$\frac{\overrightarrow{AH}}{|\overrightarrow{AH}|}$=$\frac{|\overrightarrow{AC}|×|\overrightarrow{AH}|cos＜\overrightarrow{AC}，\overrightarrow{AH}＞}{|\overrightarrow{AH}|}$
=|$\overrightarrow{AC}$|cos＜$\overrightarrow{AC}$，$\overrightarrow{AH}$＞=|$\overrightarrow{AH}$|，又csinB=|$\overrightarrow{AH}$|，∴①正确；
对于②，$\overrightarrow{BC}$•（$\overrightarrow{AC}$-$\overrightarrow{AB}$）=${\overrightarrow{BC}}^{2}$=a²，
由余弦定理知a²=b²+c²-2bccosA，∴②正确；
对于③，$\overrightarrow{AH}$•$\overrightarrow{AC}$=$\overrightarrow{AH}$•（$\overrightarrow{AH}$+$\overrightarrow{HC}$）=${\overrightarrow{AH}}^{2}$+$\overrightarrow{AH}$•$\overrightarrow{HC}$=${\overrightarrow{AH}}^{2}$，∴③正确；
对于④，$\overrightarrow{AH}$•（$\overrightarrow{AB}$+$\overrightarrow{BC}$）=$\overrightarrow{AH}$•$\overrightarrow{AC}$=${\overrightarrow{AH}}^{2}$，
$\overrightarrow{AH}$•$\overrightarrow{AB}$=$\overrightarrow{AH}$•（$\overrightarrow{AH}$+$\overrightarrow{HB}$）=${\overrightarrow{AH}}^{2}$+$\overrightarrow{AH}$•$\overrightarrow{HB}$=${\overrightarrow{AH}}^{2}$，
∴$\overrightarrow{AH}$•$\overrightarrow{AB}$+$\overrightarrow{BC}$）=$\overrightarrow{AH}$•$\overrightarrow{AB}$，④正确．
综上，正确的序号是①②③④．
故答案为：①②③④．

点评 本题考查了三角形与平面向量的相关性质，也考查了平面向量的数量积运算问题，是综合题．