
分析 由题意知,全部“三位递增数”的个数为$C_9^3=84$,随机变量X的取值为:0,-1,1,分别求出相应的概率,由此能求出X的分布列.
解答 解:由题意知,全部“三位递增数”的个数为$C_9^3=84$,
随机变量X的取值为:0,-1,1,
$P({X=0})=\frac{C_8^3}{C_9^3}=\frac{2}{3}$,
$P({X=-1})=\frac{C_4^2}{C_9^3}=\frac{1}{14}$,
$P({X=1})=1-\frac{1}{14}-\frac{2}{3}=\frac{11}{42}$
所以X的分布列为
| X | 0 | -1 | 1 |
| P | $\frac{2}{3}$ | $\frac{1}{14}$ | $\frac{11}{42}$ |
点评 本题考查离散型随机变量的分布列、古典概型等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 椭圆 | B. | 线段 | C. | 不存在 | D. | 椭圆或线段 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
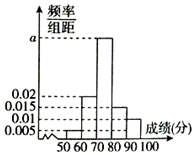 为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.
为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.| 男生 | 女生 | 合计 | |
| 优 秀 | |||
| 不优秀 | |||
| 合 计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com