
【题目】设![]() ,当
,当![]() 时,
时,![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据题意,分析可得函数f(x)为奇函数且在R为增函数,进而f(msinθ)+f(1﹣m)>0恒成立可以转化为msinθ>m﹣1,对θ的值分情况讨论,求出m的取值范围,综合即可得答案.
解:根据题意,f(x)=2x﹣sinx,
有f(﹣x)=2(﹣x)﹣sin(﹣x)=﹣(2x﹣sinx)=﹣f(x),则函数f(x)为奇函数,
又由f(x)=2x﹣sinx,则f′(x)=2﹣cosx>0,则函数f(x)在R上为增函数,
若f(msinθ)+f(1﹣m)>0恒成立,则有f(msinθ)>﹣f(1﹣m)
即f(msinθ)>f(m﹣1)恒成立,
而函数f(x)为增函数,
则有msinθ>m﹣1,
若θ![]() ,则sinθ=1,此时msinθ>m﹣1恒成立;
,则sinθ=1,此时msinθ>m﹣1恒成立;
若0![]() 时,此时msinθ>m﹣1转化为m
时,此时msinθ>m﹣1转化为m![]() ,分析可得m<1,
,分析可得m<1,
综合可得:m的取值范围是(﹣∞,1);
故选:D.


科目:高中数学 来源: 题型:
【题目】中国和印度是当今世界上两个发展最快且是最大的发展中国家,为了解两国经济的发展情况,收集了2008年至2017年两国GDP年度增长率,并绘制成如图折线图,则下列结论不正确的是( )
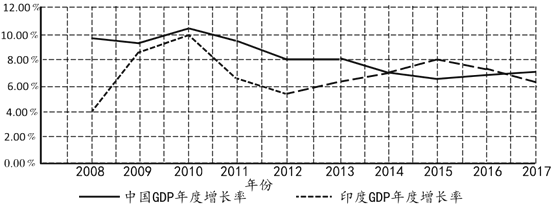
A.2010年,两国GDP年度增长率均为最大
B.2014年,两国GDP年度增长率几乎相等
C.这十年内,中国比印度的发展更为平稳一些
D.2015年起,印度GDP年度增长率均比中国大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推进“千村百镇计划”,![]() 年
年![]() 月某新能源公司开展“电动莆田 绿色出行”活动,首批投放
月某新能源公司开展“电动莆田 绿色出行”活动,首批投放![]() 台
台![]() 型新能源车到莆田多个村镇,供当地村民免费试用三个月.试用到期后,为了解男女试用者对
型新能源车到莆田多个村镇,供当地村民免费试用三个月.试用到期后,为了解男女试用者对![]() 型新能源车性能的评价情况,该公司要求每位试用者填写一份性能综合评分表(满分为
型新能源车性能的评价情况,该公司要求每位试用者填写一份性能综合评分表(满分为![]() 分).最后该公司共收回
分).最后该公司共收回![]() 份评分表,现从中随机抽取
份评分表,现从中随机抽取![]() 份(其中男、女的评分表各
份(其中男、女的评分表各![]() 份)作为样本,经统计得到如下茎叶图:
份)作为样本,经统计得到如下茎叶图:

(1)求![]() 个样本数据的中位数
个样本数据的中位数![]() ;
;
(2)已知![]() 个样本数据的平均数
个样本数据的平均数![]() ,记
,记![]() 与
与![]() 的最大值为
的最大值为![]() .该公司规定样本中试用者的“认定类型”:评分不小于
.该公司规定样本中试用者的“认定类型”:评分不小于![]() 的为“满意型”,评分小于
的为“满意型”,评分小于![]() 的为“需改进型”.
的为“需改进型”.
①请根据![]() 个样本数据,完成下面
个样本数据,完成下面![]() 列联表:
列联表:
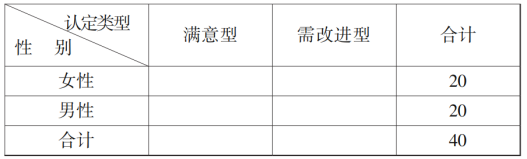
根据![]() 列联表判断能否有
列联表判断能否有![]() 的把握认为“认定类型”与性别有关?
的把握认为“认定类型”与性别有关?
②为做好车辆改进工作,公司先从样本“需改进型”的试用者按性别用分层抽样的方法,从中抽取8人进行回访,根据回访意见改进车辆后,再从这8人中随机抽取3人进行二次试用,记这3人中男性人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如题所示:扇形ABC是一块半径为2千米,圆心角为60°的风景区,P点在弧BC上,现欲在风景区中规划三条三条商业街道PQ、QR、RP,要求街道PQ与AB垂直,街道PR与AC垂直,直线PQ表示第三条街道。
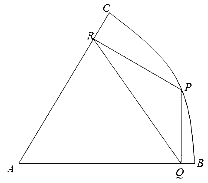
(1)如果P位于弧BC的中点,求三条街道的总长度;
(2)由于环境的原因,三条街道PQ、PR、QR每年能产生的经济效益分别为每千米300万元、200万元及400万元,问:这三条街道每年能产生的经济总效益最高为多少?(精确到1万元)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() ,离心率
,离心率![]() ,短轴
,短轴![]() ,抛物线顶点在原点,以坐标轴为对称轴,焦点为
,抛物线顶点在原点,以坐标轴为对称轴,焦点为![]() ,
,
(1)求椭圆和抛物线的方程;
(2)设坐标原点为![]() ,
,![]() 为抛物线上第一象限内的点,
为抛物线上第一象限内的点,![]() 为椭圆是一点,且有
为椭圆是一点,且有![]() ,当线段
,当线段![]() 的中点在
的中点在![]() 轴上时,求直线
轴上时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,底面是边长为
中,底面是边长为![]() 的正三角形,点
的正三角形,点![]() 在底面
在底面![]() 上的射影
上的射影![]() 恰是
恰是![]() 的中点,侧棱
的中点,侧棱![]() 和底面成
和底面成![]() 角.
角.
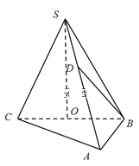
(1)若![]() 为侧棱
为侧棱![]() 上一点,当
上一点,当![]() 为何值时,
为何值时,![]() ;
;
(2)求二面角![]() 的余弦值大小.
的余弦值大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】至![]() 年底,我国发明专利申请量已经连续
年底,我国发明专利申请量已经连续![]() 年位居世界首位,下表是我国
年位居世界首位,下表是我国![]() 年至
年至![]() 年发明专利申请量以及相关数据.
年发明专利申请量以及相关数据.
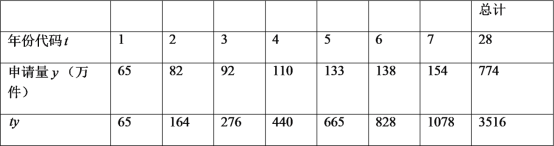
注:年份代码![]() ~
~![]() 分别表示
分别表示![]() ~
~![]() .
.
(1)可以看出申请量每年都在增加,请问这几年中哪一年的增长率达到最高,最高是多少?
(2)建立![]() 关于
关于![]() 的回归直线方程(精确到
的回归直线方程(精确到![]() ),并预测我国发明专利申请量突破
),并预测我国发明专利申请量突破![]() 万件的年份.
万件的年份.
参考公式:回归直线的斜率和截距的最小二乘法估计分别为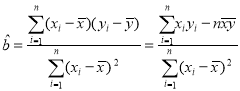 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com