
【题目】为推进“千村百镇计划”,![]() 年
年![]() 月某新能源公司开展“电动莆田 绿色出行”活动,首批投放
月某新能源公司开展“电动莆田 绿色出行”活动,首批投放![]() 台
台![]() 型新能源车到莆田多个村镇,供当地村民免费试用三个月.试用到期后,为了解男女试用者对
型新能源车到莆田多个村镇,供当地村民免费试用三个月.试用到期后,为了解男女试用者对![]() 型新能源车性能的评价情况,该公司要求每位试用者填写一份性能综合评分表(满分为
型新能源车性能的评价情况,该公司要求每位试用者填写一份性能综合评分表(满分为![]() 分).最后该公司共收回
分).最后该公司共收回![]() 份评分表,现从中随机抽取
份评分表,现从中随机抽取![]() 份(其中男、女的评分表各
份(其中男、女的评分表各![]() 份)作为样本,经统计得到如下茎叶图:
份)作为样本,经统计得到如下茎叶图:

(1)求![]() 个样本数据的中位数
个样本数据的中位数![]() ;
;
(2)已知![]() 个样本数据的平均数
个样本数据的平均数![]() ,记
,记![]() 与
与![]() 的最大值为
的最大值为![]() .该公司规定样本中试用者的“认定类型”:评分不小于
.该公司规定样本中试用者的“认定类型”:评分不小于![]() 的为“满意型”,评分小于
的为“满意型”,评分小于![]() 的为“需改进型”.
的为“需改进型”.
①请根据![]() 个样本数据,完成下面
个样本数据,完成下面![]() 列联表:
列联表:
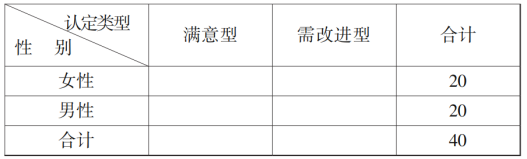
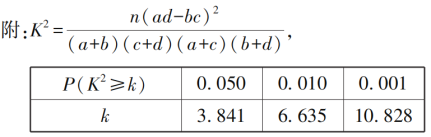
根据![]() 列联表判断能否有
列联表判断能否有![]() 的把握认为“认定类型”与性别有关?
的把握认为“认定类型”与性别有关?
②为做好车辆改进工作,公司先从样本“需改进型”的试用者按性别用分层抽样的方法,从中抽取8人进行回访,根据回访意见改进车辆后,再从这8人中随机抽取3人进行二次试用,记这3人中男性人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】(1)81;(2)①有![]() 的把握认为“认定类型”与性别有关,②见解析
的把握认为“认定类型”与性别有关,②见解析
【解析】
(1)![]() 个数字,中位数为从小到大排序的第
个数字,中位数为从小到大排序的第![]() 和第
和第![]() 数的平均数,可求得结果;(2)①将数据代入公式可求得
数的平均数,可求得结果;(2)①将数据代入公式可求得![]() ,可知
,可知![]() ,对比概率表格可知有
,对比概率表格可知有![]() 的把握认为二者相关;②通过分层抽样确定男性和女性的人数,得到
的把握认为二者相关;②通过分层抽样确定男性和女性的人数,得到![]() 所有可能的取值,根据超几何分布得到分布列,从而根据数学期望的公式求得结果.
所有可能的取值,根据超几何分布得到分布列,从而根据数学期望的公式求得结果.
(1)由茎叶图可知:![]()
(2)因为![]() ,
,![]() ,所以
,所以![]()
①由茎叶图值,女性试用者评分不小于![]() 的有
的有![]() 个,男性试用者评分不小于
个,男性试用者评分不小于![]() 的有
的有![]() 个,根据题意得
个,根据题意得![]() 列联表:
列联表:
满意型 | 需改进型 | 合计 | |
女性 |
|
|
|
男性 |
|
|
|
合计 |
|
|
|
由于![]()
查表得:![]()
所以有![]() 的把握认为“认定类型”与性别有关
的把握认为“认定类型”与性别有关
②由①知,从样本“需改进型”的试用者中按性别用分层抽样的方法抽出女性![]() 名,男性
名,男性![]() 名
名
![]() 的所有可能取值为
的所有可能取值为![]() ,
,![]() ,
,![]()
则![]() ,
,![]() ,
,
![]()
所以![]() 的分布列如下:
的分布列如下:
|
|
|
|
|
|
|
|
所以![]() 的数学期望为:
的数学期望为:![]()


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:
【题目】在实数集R中,我们定义的大小关系“>”为全体实数排了一个“序”.类似地,我们在复数集C上也可以定义一个称为“序”的关系,记为“>”.定义如下:对于任意两个复数:![]() 当且仅当“
当且仅当“![]() ”或“
”或“![]() ”且“
”且“![]() ”.按上述定义的关系“>”,给出以下四个命题:
”.按上述定义的关系“>”,给出以下四个命题:
①若![]() ,则
,则![]() ;
;
②若![]() ,则
,则![]() ;
;
③若![]() ,则对于任意
,则对于任意![]() ;
;
④对于复数![]() ,若
,若![]() ,则
,则![]() .
.
其中所有真命题的序号为______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
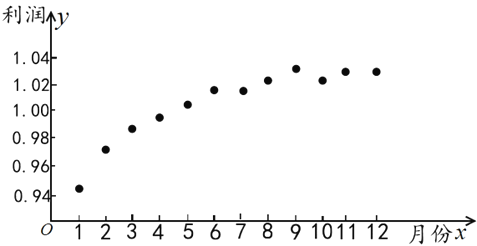
【题目】如图是某创业公司2017年每月份公司利润(单位:百万元)情况的散点图:为了预测该公司2018年的利润情况,根据上图数据,建立了利润y与月份x的两个线性回归模型:①![]() 0.94+0.028
0.94+0.028![]() ;②
;②![]() 0.96+0.032lnx,并得到以下统计值:
0.96+0.032lnx,并得到以下统计值:
模型① | 模型② | |
残差平方和 | 0.000591 | 0.000164 |
总偏差平方和 | 0.006050 | |
(1)请利用相关指数R2判断哪个模型的拟合效果更好;
(2)为了激励员工工作的积极性,公司每月会根据利润的情况进行奖惩,假设本月利润为y1,而上一月利润为y2,计算z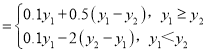 ,并规定:若z≥10,则向全体员工发放奖金总额z元;若z<10,从全体员工每人的工资中倒扣10﹣z元作为惩罚,扣完为止,请根据(1)中拟合效果更好的回归模型,试预测208年4月份该公司的奖惩情况?(结果精确到小数点后两位)
,并规定:若z≥10,则向全体员工发放奖金总额z元;若z<10,从全体员工每人的工资中倒扣10﹣z元作为惩罚,扣完为止,请根据(1)中拟合效果更好的回归模型,试预测208年4月份该公司的奖惩情况?(结果精确到小数点后两位)
参考数据及公式:![]() 1.73,
1.73,![]() 2.24,1n2≈0.69,1n3≈1.10,ln5≈1.61.相关指数R2=1
2.24,1n2≈0.69,1n3≈1.10,ln5≈1.61.相关指数R2=1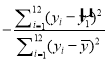 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
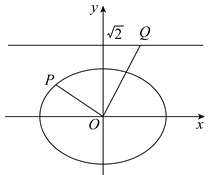
【题目】如图,在平面直角坐标系xOy中,已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点到直线
,右焦点到直线![]() 的距离为1.
的距离为1.
![]() 求椭圆的标准方程;
求椭圆的标准方程;
![]() 若P为椭圆上的一点
若P为椭圆上的一点![]() 点P不在y轴上
点P不在y轴上![]() ,过点O作OP的垂线交直线
,过点O作OP的垂线交直线![]() 于点Q,求
于点Q,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】石嘴山市第三中学高三年级统计学生的最近20次数学周测成绩(满分150分),现有甲乙两位同学的20次成绩如茎叶图所示:
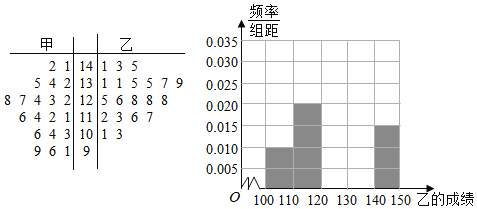
(1)根据茎叶图求甲乙两位同学成绩的中位数,并将同学乙的成绩的频率分布直方图填充完整;
(2)根据茎叶图比较甲乙两位同学数学成绩的平均值及稳定程度(不要求计算出具体值,给出结论即可);
(3)现从甲乙两位同学的不低于140分的成绩中任意选出2个成绩,记事件![]() 为“其中2个成绩分别属于不同的同学”,求事件
为“其中2个成绩分别属于不同的同学”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,过点
,过点![]() 作直线
作直线![]() 和曲线
和曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求曲线![]() 的焦点到它的渐近线之间的距离;
的焦点到它的渐近线之间的距离;
(2)若![]() ,点
,点![]() 在第一象限,
在第一象限,![]() 轴,垂足为
轴,垂足为![]() ,连结
,连结![]() ,求直线
,求直线![]() 倾斜角的取值范围;
倾斜角的取值范围;
(3)过点![]() 作另一条直线
作另一条直线![]() ,
,![]() 和曲线
和曲线![]() 交于
交于![]() 、
、![]() 两点,问是否存在实数
两点,问是否存在实数![]() ,使得
,使得![]() 和
和![]() 同时成立?如果存在,求出满足条件的实数
同时成立?如果存在,求出满足条件的实数![]() 的取值集合,如果不存在,请说明理由.
的取值集合,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)已知![]() 是以2为周期的偶函数,且当
是以2为周期的偶函数,且当![]() 时,有
时,有![]() .若
.若![]() ,且
,且![]() ,求函数
,求函数![]()
![]() 的反函数;
的反函数;
(3)若在![]() 上存在
上存在![]() 个不同的点
个不同的点![]() ,
,![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com