【题目】某农场预算用5600元购买单价为50元（每吨）的钾肥和20元（每吨）的氮肥，希望使两种肥料的总数量（吨）尽可能的多，但氮肥数不少于钾肥数，且不多于钾肥数的1.5倍
(Ⅰ)设买钾肥
吨，买氮肥
吨，按题意列出约束条件、画出可行域，并求钾肥、氮肥各买多少才行？
(Ⅱ)已知
，
是坐标原点， 
在(Ⅰ)中的可行域内，求
的取值范围.
【答案】(Ⅰ) 购买钾肥70吨，氮肥105吨时，两种肥料的总数量最大为175吨(Ⅱ)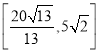 
【解析】
试题分析：(Ⅰ)首先由已知条件中的限定条件可得到关于x,y的不等式，从而确定线性约束条件，进而由不等式得到可行域，通过对目标函数
的变形，将z赋予特定的几何含义：直线的截距，从而求得z取最值时x,y的取值；(Ⅱ) 将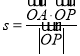
代入点的坐标转化为
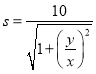，借助于斜率求解s的取值范围
试题解析：(Ⅰ)设肥料总数为
，
由题意得约束条件
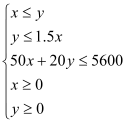，即
画出可行域（如图）
目标函数：，即
，
表示斜率为
，
轴上截距为
的平行直线系.
当直线过点N时，
最大.
联立方程
，解得
此时
.
购买钾肥70吨，氮肥105吨时，两种肥料的总数量最大为175吨
(Ⅱ)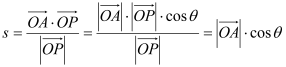
，
，
为
的夹角
.有图可知：
当点
在线段
时，
最大为
，此时s最大值为
；
当点
在线段
时，最小为
，此时s最小值为
.
另解：
，
，代入可得
计算高手系列答案科目：高中数学 来源： 题型：
【题目】下列每组对象能构成集合的是（ ）
A.铜仁一中“迎国庆，大合唱”比赛中，唱的非常好的班级.
B.“文明在行动，满意在铜中”专项活动中，表现好的学生.
C.高一（16）班，年龄大于15岁的同学.
D.铜仁一中校园内，美丽的小鸟.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝x3－12x＋a，其中a≥16，则下列说法正确的是( )．
A．f(x)有且只有一个零点
B．f(x)至少有两个零点
C．f(x)最多有两个零点
D．f(x)一定有三个零点
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（多选）某小组有三名男生和两名女生，从中任选两名去参加比赛，则下列各对事件中为互斥事件的是（ ）
A.恰有一名男生和全是男生B.至少有一名男生和至少有一名女生
C.至少有一名男生和全是男生D.至少有一名男生和全是女生
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】学校为测评班级学生对任课教师的满意度，采用“100分制”打分的方式来计分，规定满意度不低于98分，则评价该教师为“优秀”，现从某班学生中随机抽取10名，以下茎叶图记录了他们对某教师的满意度分数（以十位数字为茎，个位数字为叶）；
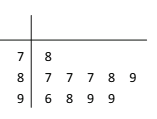
（1）指出这组数据的众数和中位数；
（2）求从这10人中随机选取3人，至多有1人评价该教师是“优秀”的概率；
（3）以这10人的样本数据来估计整个班级的总体数据，若从该班任选3人，记
表示抽到评价该教师为“优秀”的人数，求
的分布列及数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知关于
的方程为
．
（Ⅰ）若
，
，求方程有实数根的概率.
（Ⅱ）若
，，求方程有实数根的概率.
（Ⅲ）在区间
上任取两个数
和
，利用随机数模拟的方法近似计算关于的方程有实数根的概率，请写出你的试验方法.
查看答案和解析>>
科目：高中数学 来源： 题型：
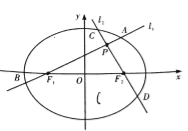
【题目】如图，分别过椭圆
左、右焦点
的动直线
相交于
点，与椭圆
分别交于
与
不同四点，直线
的斜率
满足
, 已知
与
轴重合时, 
.
（1）求椭圆
的方程；
（2）是否存在定点
使得
为定值，若存在，求出点坐标并求出此定值，若不存在，
说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】光线通过一块玻璃，其强度要损失10%，把几块这样的玻璃重叠起来，设光线原来的强度为
，通过
块玻璃以后强度为
.
（Ⅰ）写出关于的函数关系式；
（Ⅱ）通过多少块玻璃以后，光线强度减弱到原来的
以下.（lg3≈0.4771）.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
