
【题目】学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分,规定满意度不低于98分,则评价该教师为“优秀”,现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶);
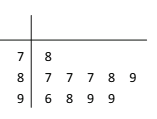
(1)指出这组数据的众数和中位数;
(2)求从这10人中随机选取3人,至多有1人评价该教师是“优秀”的概率;
(3)以这10人的样本数据来估计整个班级的总体数据,若从该班任选3人,记![]() 表示抽到评价该教师为“优秀”的人数,求
表示抽到评价该教师为“优秀”的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】从装有4个红球和3个白球的袋中任取2个球,那么下列事件中,是对立事件的是( )
A.至少有1个白球;都是红球B.至少有1个白球;至少有1个红球
C.恰好有1个白球;恰好有2个白球D.至少有1个白球;都是白球
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校将5个参加知识竞赛的名额全部分配给高二年级的4个班级,其中甲班级至少分配2个名额,其它班级可以不分配名额或分配多个名额,则不同的分配方案共有( )
A.30种 B.26种 C.24种 D.20种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场预算用5600元购买单价为50元(每吨)的钾肥和20元(每吨)的氮肥,希望使两种肥料的总数量(吨)尽可能的多,但氮肥数不少于钾肥数,且不多于钾肥数的1.5倍
(Ⅰ)设买钾肥![]() 吨,买氮肥
吨,买氮肥![]() 吨,按题意列出约束条件、画出可行域,并求钾肥、氮肥各买多少才行?
吨,按题意列出约束条件、画出可行域,并求钾肥、氮肥各买多少才行?
(Ⅱ)已知![]() ,
,![]() 是坐标原点,
是坐标原点, ![]() 在(Ⅰ)中的可行域内,求
在(Ⅰ)中的可行域内,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对一批电子元件进行寿命追踪调查,从这批产品中抽取![]() 个产品(其中
个产品(其中![]() ),得到频率分布直方图如下:
),得到频率分布直方图如下:

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)从频率分布直方图估算这批电子元件寿命的平均数、中位数的估计分别是多少?
(Ⅲ)现要从300![]() 400及400
400及400![]() 500这两组中按照分层抽样的方法抽取一个样本容量为36的样本,则在300
500这两组中按照分层抽样的方法抽取一个样本容量为36的样本,则在300![]() 400及400
400及400![]() 500这两组分别抽多少件产品.
500这两组分别抽多少件产品.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面五边形![]() 是轴对称图形(如图1),BC为对称轴,AD⊥CD,AD=AB=1,
是轴对称图形(如图1),BC为对称轴,AD⊥CD,AD=AB=1,![]() ,将此五边形沿BC折叠,使平面ABCD⊥平面BCEF,得到如图2所示的空间图形,对此空间图形解答下列问题.
,将此五边形沿BC折叠,使平面ABCD⊥平面BCEF,得到如图2所示的空间图形,对此空间图形解答下列问题.
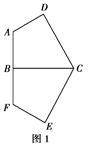
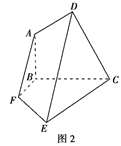
(1)证明:AF∥平面DEC;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 在它的某一个周期内的单调减区间是
在它的某一个周期内的单调减区间是![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)将![]() 的图象先向右平移
的图象先向右平移![]() 个单位,再将图象上所有点的横坐标变为原来的
个单位,再将图象上所有点的横坐标变为原来的![]() 倍(纵坐标不变),所得到的图象对应的函数记为
倍(纵坐标不变),所得到的图象对应的函数记为![]() ,若对于任意的
,若对于任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com