
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 通过分析残差有利于发现样本数据中的可疑数据 | |
| B. | 根据获取的样本数据计算${\sum_{i=1}^n{({{y_i}-\overline y})}^2}$,若${\sum_{i=1}^n{({{y_i}-\overline y})}^2}$越小,则模型的拟合效果越好 | |
| C. | 根据获取的样本数据计算$\sum_{i=1}^n{{{({{y_i}-\hat y})}^2}}$,若$\sum_{i=1}^n{{{({{y_i}-\hat y})}^2}}$越大,则模型的拟合效果越差 | |
| D. | 根据获取的样本数据计算R2,若R2=0.85,则表明解释变量解释了85%的预报变量变化 |
查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 0040 | B. | 0795 | C. | 0815 | D. | 0420 |
查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:解答题
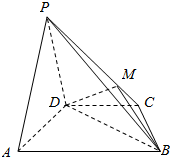 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4,BD=4$\sqrt{3}$,AB=2CD=8.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4,BD=4$\sqrt{3}$,AB=2CD=8.查看答案和解析>>
科目: 来源: 题型:解答题
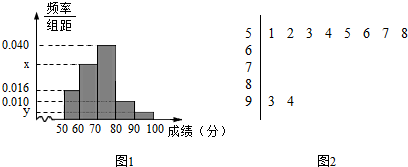
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com