
科目: 来源:2017届江苏苏州市高三期中调研数学试卷(解析版) 题型:解答题
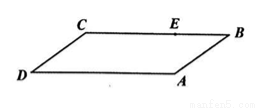
如图,有一块平行四边形绿地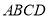 ,经测量
,经测量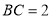 百米,
百米, 百米,
百米,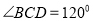 ,拟过线段
,拟过线段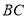 上一点
上一点 设计一条直路
设计一条直路 (点
(点 在四边形
在四边形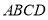 的边上,不计路的宽度),
的边上,不计路的宽度), 将绿地分成两部分,且右边面积是左边面积的3倍,设
将绿地分成两部分,且右边面积是左边面积的3倍,设 百米,
百米,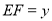 百米.
百米.
(1)当点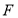 与点
与点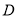 重合时,试确定点
重合时,试确定点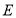 的位置;
的位置;
(2)试求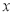 的值,使路
的值,使路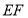 的长度
的长度 最短.
最短.
查看答案和解析>>
科目: 来源:2017届江苏苏州市高三期中调研数学试卷(解析版) 题型:解答题
已知数列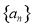 的前
的前 项和为
项和为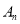 ,对任意
,对任意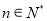 满足
满足 ,且
,且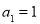 ,数列
,数列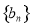 满足
满足 ,其前9项和为63.
,其前9项和为63.
(1)求数列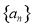 和
和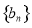 的通项公式;
的通项公式;
(2)令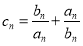 ,数列
,数列 的前
的前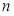 项和为
项和为 ,若对任意正整数
,若对任意正整数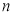 ,都有
,都有 ,求实数
,求实数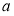 的取值范围;
的取值范围;
(3)将数列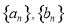 的项按照“当
的项按照“当 为奇数时,
为奇数时,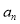 放在前面;当
放在前面;当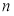 为偶数时,
为偶数时, 放在前面”的要求进行“交叉排列”,得到一个新的数列:
放在前面”的要求进行“交叉排列”,得到一个新的数列: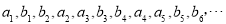 ,求这个新数列的前
,求这个新数列的前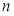 项和
项和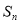 .
.
查看答案和解析>>
科目: 来源:2017届江苏苏州市高三期中调研数学试卷(解析版) 题型:解答题
已知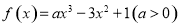 ,定义
,定义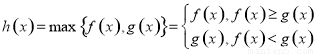 .
.
(1)求函数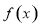 的极值;
的极值;
(2)若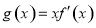 ,且存在
,且存在 使
使 ,求实数
,求实数 的取值范围;
的取值范围;
(3)若 ,试讨论函数
,试讨论函数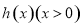 的零点个数.
的零点个数.
查看答案和解析>>
科目: 来源:2017届江苏苏州市高三期中调研数学试卷(解析版) 题型:解答题
已知二阶矩阵 有特征值
有特征值 及对应的一个特征向量
及对应的一个特征向量 ,并且矩阵
,并且矩阵 将点
将点 变换为
变换为 .
.
(1)求矩形 ;
;
(2)求曲线 在
在 的作用下的新曲线方程.
的作用下的新曲线方程.
查看答案和解析>>
科目: 来源:2017届江苏苏州市高三期中调研数学试卷(解析版) 题型:解答题
已知平面直角坐标系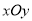 中,圆
中,圆 的参数方程为
的参数方程为 (
(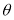 为参数,
为参数, ).以直角坐标系原点
).以直角坐标系原点 为极点,
为极点,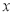 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线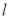 的极坐标方程为
的极坐标方程为 .
.
(1)求圆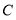 的圆心的极坐标;
的圆心的极坐标;
(2)当圆 与直线
与直线 有公共点时,求
有公共点时,求 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2017届江苏苏州市高三期中调研数学试卷(解析版) 题型:解答题
某公司对新招聘的员工张某进行综合能力测试,共设置了 三个测试项目,假定张某通过项目
三个测试项目,假定张某通过项目 的概率为
的概率为 ,通过项目
,通过项目 的概率均为
的概率均为 ,且这三个测试项目能否通过相互独立.
,且这三个测试项目能否通过相互独立.
(1)用随机变量 表示张某在测试中通过的项目个数,求
表示张某在测试中通过的项目个数,求 的概率分布和数学期望
的概率分布和数学期望 (用
(用 表示);
表示);
(2)若张某通过一个项目的概率最大,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2017届江苏苏州市高三期中调研数学试卷(解析版) 题型:解答题
在如图所示的四棱锥 中,
中,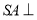 底面
底面 ,
, 为线段
为线段 上的一个动点.
上的一个动点.
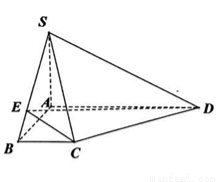
(1)证明 : 和
和 不可能垂直;
不可能垂直;
(2)当点 为线段
为线段 的三等分点(靠近
的三等分点(靠近 )时,求二面角
)时,求二面角 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com