
科目: 来源:2017届河南省洛阳市高三第二次统一考试(3月)数学(理)试卷(解析版) 题型:选择题
已知函数 ,关于
,关于 的方程
的方程 ,有
,有 个不同的实数解,则
个不同的实数解,则 的取值范围是( )
的取值范围是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源:2017届河南省洛阳市高三第二次统一考试(3月)数学(理)试卷(解析版) 题型:填空题
意大利著名数学家斐波那契在研究兔子的繁殖问题时,发现有这样的一列数: .该数列的特点是:前两个数均为
.该数列的特点是:前两个数均为 ,从第三个数起,每一个数都等于它前面两个数的和,人们把这样的一列数所组成的数列
,从第三个数起,每一个数都等于它前面两个数的和,人们把这样的一列数所组成的数列 称为“斐波那契数列”,则
称为“斐波那契数列”,则


 ______.
______.
查看答案和解析>>
科目: 来源:2017届河南省洛阳市高三第二次统一考试(3月)数学(理)试卷(解析版) 题型:填空题
如图,扇形 的弧的中点为
的弧的中点为 ,动点
,动点 ,
, 分别在线段
分别在线段 ,
, 上,且
上,且 ,若
,若 ,
, ,则
,则 的取值范围是______.
的取值范围是______.

查看答案和解析>>
科目: 来源:2017届河南省洛阳市高三第二次统一考试(3月)数学(理)试卷(解析版) 题型:填空题
已知椭圆 的左、右顶点分别为
的左、右顶点分别为 、
、 ,
, 为椭圆
为椭圆 的右焦点.圆
的右焦点.圆 上有一动点
上有一动点 ,
, 不同于
不同于 ,
, 两点,直线
两点,直线 与椭圆
与椭圆 交于点
交于点 ,则
,则 的取值范围是______.
的取值范围是______.
查看答案和解析>>
科目: 来源:2017届河南省洛阳市高三第二次统一考试(3月)数学(理)试卷(解析版) 题型:解答题
已知数列 中,
中, ,其前
,其前 项和为
项和为 ,且满足
,且满足 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)记 ,若数列
,若数列 为递增数列,求
为递增数列,求 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2017届河南省洛阳市高三第二次统一考试(3月)数学(理)试卷(解析版) 题型:解答题
某厂有4台大型机器,在一个月中,一台机器至多出现1次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修,每台机器出现故障需要维修的概率为 .
.
(1)若出现故障的机器台数为 ,求
,求 的分布列;
的分布列;
(2) 该厂至少有多少名工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不少于90%?
(3)已知一名工人每月只有维修1台机器的能力,每月需支付给每位工人1万元的工资,每台机器不出现故障或出现故障能及时维修,就使该厂产生5万元的利润,否则将不产生利润,若该厂现有2名工人,求该厂每月获利的均值.
查看答案和解析>>
科目: 来源:2017届河南省洛阳市高三第二次统一考试(3月)数学(理)试卷(解析版) 题型:解答题
已知三棱锥 ,
, 平面
平面 ,
,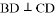 ,
, ,
, ,
, ,
, 分别是
分别是 ,
, 的中点.
的中点.

(1) 为线段
为线段 上一点.且
上一点.且 ,求证:
,求证: .
.
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com