
科目: 来源: 题型:
【题目】已知数列![]() 满足:对于任意
满足:对于任意![]() 且
且![]() 时,
时,![]() ,
,![]() .
.
(1)若![]() ,求证:
,求证:![]() 为等比数列;
为等比数列;
(2)若![]() .
.
① 求数列![]() 的通项公式;
的通项公式;
② 是否存在![]() ,使得
,使得![]() 为数列
为数列![]() 中的项?若存在,求出所有满足条件的
中的项?若存在,求出所有满足条件的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
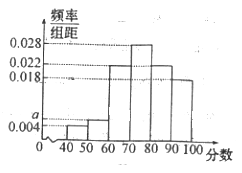
【题目】某学校为了解学校食堂的服务情况,随机调查了50名就餐的教师和学生.根据这50名师生对餐厅服务质量进行评分,绘制出了频率分布直方图(如图所示),其中样本数据分组为![]() .
.
(1)求频率分布直方图中![]() 的值;
的值;
(2)从评分在![]() 的师生中,随机抽取2人,求此人中恰好有1人评分在
的师生中,随机抽取2人,求此人中恰好有1人评分在![]() 上的概率;
上的概率;
(3)学校规定:师生对食堂服务质量的评分不得低于75分,否则将进行内部整顿,试用组中数据估计该校师生对食堂服务质量评分的平均分,并据此回答食堂是否需要进行内部整顿.
查看答案和解析>>
科目: 来源: 题型:
【题目】网络购物已经被大多数人接受,随着时间的推移,网络购物的人越来越多,然而也有部分人对网络购物的质量和信誉产生怀疑。对此,某新闻媒体进行了调查,在所有参与调查的人中,持“支持”和“不支持”态度的人数如下表所示:
年龄 态度 | 支持 | 不支持 |
20岁以上50岁以下 | 800 | 200 |
50岁以 (含50岁) | 100 | 300 |
(1)在所有参与调查的人中,用分层抽样的方法抽取![]() 个人,已知从持“支持”态度的人中抽取了9人,求
个人,已知从持“支持”态度的人中抽取了9人,求![]() 的值;
的值;
(2)是否有99.9%的把握认为支持网络购物与年龄有关?
参考数据:
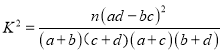 ,其中
,其中![]() ,
,
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() 且满足
且满足![]() ,数列
,数列![]() 中,
中,![]() 对任意正整数
对任意正整数![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)是否存在实数![]() ,使得数列
,使得数列![]() 是等比数列?若存在,请求出实数
是等比数列?若存在,请求出实数![]() 及公比
及公比![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)求证:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建设一仓库,设![]() ,并在公路北侧建造边长为
,并在公路北侧建造边长为![]() 的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且
的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式,并求出定义域;
的函数解析式,并求出定义域;
(2)如果中转站四堵围墙造价为10万元/km,两条道路造价为30万元/km,问:![]() 取何值时,该公司建设中转站围墙和两条道路总造价M最低.
取何值时,该公司建设中转站围墙和两条道路总造价M最低.

查看答案和解析>>
科目: 来源: 题型:
【题目】某企业准备投入适当的广告费对产品进行促销,在一年内预计销售量Q(万件)与广告费x(万元)之间的函数关系为Q=![]() (x>1),已知生产该产品的年固定投入为3万元,每生产1万件该产品另需再投入32万元,若每件销售价为“年平均每件生产成本(生产成本不含广告费)的150%”与“年平均每件所占广告费的50%”之和.
(x>1),已知生产该产品的年固定投入为3万元,每生产1万件该产品另需再投入32万元,若每件销售价为“年平均每件生产成本(生产成本不含广告费)的150%”与“年平均每件所占广告费的50%”之和.
(1)试将年利润W(万元)表示为年广告费x(万元)的函数;(年利润=销售收入-成本)
(2)当年广告费为多少万元时,企业的年利润最大?最大年利润为多少万元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ABC=60°,∠BAC=90°,AD是BC边上的高,沿AD将△ABC折成60°的二面角B-AD-C,如图2.
(1)证明:平面ABD⊥平面BCD;
(2)设E为BC的中点,BD=2,求异面直线AE与BD所成的角的大小.

查看答案和解析>>
科目: 来源: 题型:
【题目】有外形相同的球分装三个盒子,每盒10个.其中,第一个盒子中7个球标有字母A、3个球标有字母B;第二个盒子中有红球和白球各5个;第三个盒子中则有红球8个,白球2个.试验按如下规则进行:先在第一号盒子中任取一球,若取得标有字母A的球,则在第二号盒子中任取一个球;若第一次取得标有字母B的球,则在第三号盒子中任取一个球.如果第二次取出的是红球,则称试验成功,那么试验成功的概率为( )
A.0.59 B.0.54 C.0.8 D.0.15
查看答案和解析>>
科目: 来源: 题型:
【题目】某高校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布如图所示.
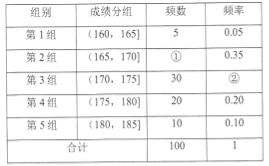
(1)请先求出频率分布表中①、②位置相应的数据,再画出频率分布直方图;
(2)该高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受考官的面试,求第4组至少有一名学生被考官面试的概率?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数![]() 的对称轴为
的对称轴为![]() ,
,![]() .
.
(1)求函数![]() 的最小值及取得最小值时
的最小值及取得最小值时![]() 的值;
的值;
(2)试确定![]() 的取值范围,使
的取值范围,使![]() 至少有一个实根;
至少有一个实根;
(3)当![]() 时,
时,![]() ,对任意
,对任意![]() 有
有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com