如图，在正四面体中，分别是棱的中点.

（1）求证：四边形是平行四边形；

（2）求证：平面；

（3）求证：平面.

【题目】【2014天津，文19】已知函数

（1） 求的单调区间和极值；

（2）若对于任意的，都存在，使得，求的取值范围

【题目】已知二次函数（其中）满足下列3个条件:

①函数的图象过坐标原点；

②函数的对称轴方程为；

③方程有两个相等的实数根，

令.

（1）求函数的解析式；

（2）求使不等式恒成立的实数的取值范围；

（3）已知函数在上的最小值为，求实数的值.

在平面直角坐标系中，有三个点的坐标分别是.

（1）证明：A，B，C三点不共线；

（2）求过A，B的中点且与直线平行的直线方程；

（3）设过C且与AB所在的直线垂直的直线为，求与两坐标轴围成的三角形的面积.

【题目】已知6只小白鼠有1只被病毒感染，需要通过对其化验病毒来确定是否感染.下面是两种化验方案：方案甲：逐个化验，直到能确定感染为止.方案乙：将6只分为两组，每组三个，并将它们混合在一起化验，若存在病毒，则表明感染在这三只当中，然后逐个化验，直到确定感染为止；若结果不含病毒，则在另外一组中逐个进行化验.

（1）求依据方案乙所需化验恰好为2次的概率.

（2）首次化验化验费为10元，第二次化验化验费为8元，第三次及其以后每次化验费都是6元，列出方案甲所需化验费用的分布列，并估计用方案甲平均需要体验费多少元？

有时可用函数

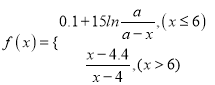
描述学习某学科知识的掌握程度，其中x表示某学科知识的学习次数（），表示对该学科知识的掌握程度，正实数a与学科知识有关.

（1） 证明：当时，掌握程度的增加量总是下降；

（2） 根据经验，学科甲、乙、丙对应的a的取值区间分别为,,

.当学习某学科知识6次时，掌握程度是85%，请确定相应的学科.

【题目】某研究小组在电脑上进行人工降雨模拟实验，准备用、、三种人工降雨方式分别对甲、乙、丙三地实施人工降雨，其试验数据统计如表：

假定对甲、乙、丙三地实施的人工降雨彼此互不影响，请你根据人工降雨模拟实验的统计数据：

（Ⅰ）求甲、乙、丙三地都恰为中雨的概率；

（Ⅱ）考虑到旱情和水土流失，如果甲地恰需中雨即达到理想状态，乙地必须是大雨才达到理想状态，丙地只能是小雨或中雨即达到理想状态，记“甲、乙、丙三地中达到理想状态的个数”为随机变量，求随机变量的分布列和数学期望．

设椭圆的离心率为，其左焦点与抛物线的焦点相同.

（1）求此椭圆的方程；

（2）若过此椭圆的右焦点的直线与曲线只有一个交点，则

①求直线的方程；

②椭圆上是否存在点，使得，若存在，请说明一共有几个点；若不存在，请说明理由.

【题目】【2014高考陕西版文第21题】设函数.

（1）当（为自然对数的底数）时，求的最小值；

（2）讨论函数零点的个数；

（3）若对任意恒成立，求的取值范围.