【题目】已知函数 在区间内单调递减，在区间内单调递增，且在上有三个零点，1是其中一个零点.

（1）求的取值范围；

（2）若直线在曲线的上方部分所对应的的集合为，试求实数的取值范围.

【题目】已知函数.

（1）求曲线在点处的切线方程；

（2）若函数在上单调递增，求实数的取值范围.

①该二项展开式中非常数项的系数和是1；

②该二项展开式中第六项为x1999；

③该二项展开式中系数最大的项是第1002项；

④当x=2006时，(x－1)2005除以2006的余数是2005。

其中正确命题的序号是__________。（注：把你认为正确的命题序号都填上）

【题目】如图，已知四棱锥的底面为菱形， ， ， .

（Ⅰ）求证： ；

（Ⅱ）求二面角的余弦值.

【题目】甲、乙二人做射击游戏，甲、乙射击击中与否是相互独立事件．规则如下：若射击一次击中，则原射击人继续射击；若射击一次不中，就由对方接替射击．已知甲、乙二人射击一次击中的概率均为，且第一次由甲开始射击．①求前3次射击中甲恰好击中2次的概率____________；②求第4次由甲射击的概率________．

【题目】某次考试中，语文成绩服从正态分布，数学成绩的频率分布直方图如下：

（Ⅰ）如果成绩大于135的为特别优秀，随机抽取的500名学生在本次考试中语文、数学成绩特别优秀的大约各多少人？（假设数学成绩在频率分布直方图中各段是均匀分布的）

（Ⅱ）如果语文和数学两科都特别优秀的共有6人，从（Ⅰ）中至少有一科成绩特别优秀的同学中随机抽取3人，设3人中两科都特别优秀的有人，求的分布列和数学期望；

（Ⅲ）根据以上数据，是否有99%的把握认为语文特别优秀的同学，数学也特别优秀.

（附公及表）

①若，则， ；

②， ；

③

【题目】已知椭圆和直线： ，椭圆的离心率，坐标原点到直线的距离为.

（Ⅰ）求椭圆的方程；

（Ⅱ）已知定点，若直线过点且与椭圆相交于两点，试判断是否存在直线，使以为直径的圆过点？若存在，求出直线的方程；若不存在，请说明理由.

【题目】已知 ,,其中(e是自然常数),

（1）当时, 求的单调区间、极值；

（2）是否存在，使的最小值是3，若存在求出的值，若不存在，说明理由.

(1)点P(4,5)关于直线l的对称点坐标；

(2)直线l1：y＝x－2关于直线l的对称直线的方程；

(3)直线l关于点A(3,2)的对称直线的方程．

【题目】为了研究一种昆虫的产卵数和温度是否有关，现收集了7组观测数据列于下表中，并作出了散点图，发现样本点并没有分布在某个带状区域内，两个变量并不呈线性相关关系，现分别用模型①：与模型②：作为产卵数和温度的回归方程来建立两个变量之间的关系.

其中， ， ， ，

附：对于一组数据，其回归直线的斜率和截距的最小二乘估计分别为： ， .

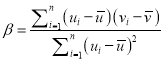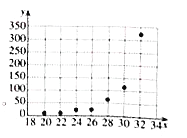
（1）在答题卡中分别画出关于的散点图、关于的散点图，根据散点图判断哪一个模型更适宜作为回归方程类型？（给出判断即可，不必说明理由）.

（2）根据表中数据，分别建立两个模型下建立关于的回归方程；并在两个模型下分别估计温度为时的产卵数.（与估计值均精确到小数点后两位）（参考数据： ， ， ）

（3）若模型①、②的相关指数计算得分分别为， ，请根据相关指数判断哪个模型的拟合效果更好.