
科目: 来源: 题型:
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查得到如下列联表:
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
合计 | 30 |
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为![]() .
.
(1)请将上面的列表补充完整;
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(3)4名调查人员随机分成两组,每组2人,一组负责问卷调查,另一组负责数据处理,求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: 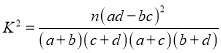 )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图. 图中A点表示十月的平均最高气温约为![]() ,B点表示四月的平均最低气温约为
,B点表示四月的平均最低气温约为![]() . 下面叙述不正确的是 ( )
. 下面叙述不正确的是 ( )

A. 各月的平均最低气温都在![]() 以上
以上
B. 七月的平均温差比一月的平均温差大
C. 三月和十一月的平均最高气温基本相同
D. 平均最高气温高于![]() 的月份有5个
的月份有5个
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别为圆
,左、右焦点分别为圆![]() ,
, ![]() 是
是![]() 上一点,
上一点, ![]() ,且
,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)当过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于不同两点
相交于不同两点![]() 时,线段
时,线段![]() 上取点
上取点![]() ,且
,且![]() 满足
满足![]() ,证明点
,证明点![]() 总在某定直线上,并求出该定直线.
总在某定直线上,并求出该定直线.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将上表的数据进行了处理, ![]() 得到下表2:
得到下表2:
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(Ⅰ)求z关于t的线性回归方程;
(Ⅱ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中 )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知△OAB的顶点坐标为O(0,0),A(2,9),B(6,﹣3),点P的横坐标为14,且 ![]() =λ
=λ ![]() ,点Q是边AB上一点,且
,点Q是边AB上一点,且 ![]()
![]() =0.
=0.
(1)求实数λ的值与点P的坐标;
(2)求点Q的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,曲线![]() 的方程为
的方程为![]() .以坐标原点为极点,
.以坐标原点为极点, ![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在曲线
在曲线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,求
上,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示. 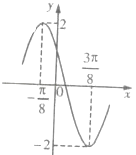
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调增区间;
(3)求函数f(x)在[﹣ ![]() ,
, ![]() ]上的单调减区间.
]上的单调减区间.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]()
![]() 的
的
部分图像如图所示.
(Ⅰ)求函数![]() 的解析式及
的解析式及![]() 图像的对称轴方程;
图像的对称轴方程;
(Ⅱ)把函数![]() 图像上点的横坐标扩大到原来的
图像上点的横坐标扩大到原来的![]() 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移
![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求关于
的图象,求关于![]() 的方程
的方程![]()
在![]() 时所有的实数根之和.
时所有的实数根之和.

查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)判断直线![]() 与曲线
与曲线![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若直线![]() 和曲线
和曲线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com