
科目: 来源: 题型:
【题目】(本小题满分12分) 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过![]() ):
):
空气质量指数 |
|
|
|
|
|
|
空气质量等级 |
|
|
|
|
|
|
该社团将该校区在![]() 年
年![]() 天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
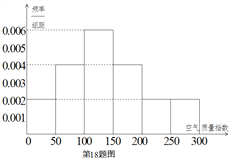
(Ⅰ)请估算![]() 年(以
年(以![]() 天计算)全年空气质量优良的天数(未满一天按一天计算);
天计算)全年空气质量优良的天数(未满一天按一天计算);
(Ⅱ)该校![]() 年
年![]() 月
月![]() 、
、![]() 日将作为高考考场,若这两天中某天出现
日将作为高考考场,若这两天中某天出现![]() 级重度污染,需要净化空气费用
级重度污染,需要净化空气费用![]() 元,出现
元,出现![]() 级严重污染,需要净化空气费用
级严重污染,需要净化空气费用![]() 元,记这两天净化空气总费用为
元,记这两天净化空气总费用为![]() 元,求
元,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义在R上的偶函数f(x)满足f(x+1)= ![]() ,且f(x)在[﹣3,﹣2]上是减函数,若α,β是锐角三角形的两个内角,则( )
,且f(x)在[﹣3,﹣2]上是减函数,若α,β是锐角三角形的两个内角,则( )
A.f(sinα)>f(sinβ)
B.f(cosα)>f(cosβ)
C.f(sinα)>f(cosβ)
D.f(sinα)<f(cosβ)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=|x﹣a|﹣ ![]() +a,x∈[1,6],a∈R.
+a,x∈[1,6],a∈R.
(1)若a=1,试判断并证明函数f(x)的单调性;
(2)当a∈(1,6)时,求函数f(x)的最大值的表达式M(a).
查看答案和解析>>
科目: 来源: 题型:
【题目】在等差数列{an}中,a1=3,其前n项和为Sn , 等比数列{bn}的各项均为正数,b1=1,公比为q(q≠0),且b2+S2=12, ![]() .
.
(1)求{an}与{bn}的通项公式;
(2)证明: ![]()
![]() +
+ ![]() +…+
+…+ ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
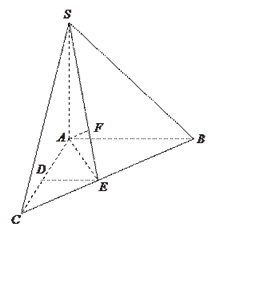
【题目】如图,在三棱锥![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,
的中点, ![]() 在
在![]() 上,且
上,且![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)在线段上![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角
![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)= ![]() 为偶函数
为偶函数
(1)求实数a的值;
系;
(2)记集合E={y|y=f(x),x∈{﹣1,1,2}},λ=lg22+lg2lg5+lg5﹣ ![]() ,判断λ与E的
,判断λ与E的
(3)当x∈[ ![]() ,
, ![]() ](m>0,n>0)时,若函数f(x)的值域[2﹣3m,2﹣3n],求实数m,n值.
](m>0,n>0)时,若函数f(x)的值域[2﹣3m,2﹣3n],求实数m,n值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com