【题目】某大学在开学季准备销售一种盒饭进行试创业，在一个开学季内，每售出1盒该盒饭获利润10元，未售出的产品，每盒亏损5元．根据历史资料，得到开学季市场需求量的频率分布直方图，如图所示．该同学为这个开学季购进了150盒该产品，以（单位：盒，）表示这个开学季内的市场需求量，（单位：元）表示这个开学季内经销该产品的利润．

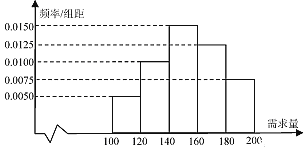
（Ⅰ）根据直方图估计这个开学季内市场需求量的平均数和众数；

（Ⅱ）将表示为的函数；

（Ⅲ）根据频率分布直方图估计利润不少于1350元的概率．

【题目】已知某扇形的面积为4cm2 ， 周长为8cm，则此扇形圆心角的弧度数是；若点（a，9）在函数y=3x的图象上，则不等式 的解集为 ．

【题目】已知三棱锥的各棱长都相等，为中点，则异面直线与所成角的余弦值为( )

A. B. C. D.

【题目】已知数列和满足： .

（1）若，求数列的通项公式；

（2）若.

求证：数列为等差数列；

记数列的前项和为，求满足的所有正整数和的值.

【题目】从某小学随机抽取100名同学，将他们的身高（单位：厘米）数据绘制成频率分布直方图由图中数据可知身高在[120，130]内的学生人数为（ ）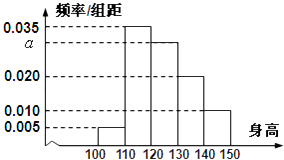

A.20
B.25
C.30
D.35

【题目】己知f（x）=x2﹣2x+2，在[ ，m2﹣m+2]上任取三个数a，b，c，均存在以 f（a），f（b），f（c）为三边的三角形，则m的取值范围为（ ）
A.（0，1）
B.[0， ）
C.（0， ]
D.[ ， ]

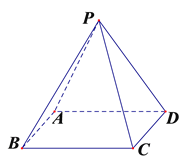
【题目】如图在四棱锥P-ABCD中，底面ABCD为矩形，侧面PAD底面ABCD， ；

（1）求证：平面PAB平面PCD；

（2）若过点B的直线垂直平面PCD，求证： //平面PAD.

【题目】已知函数在点处的切线方程为， （其中为常数）.

（1）求函数的解析式；

（2）若对任意，不等式恒成立，求实数的取值范围；

（3）当时，求证： （其中e为自然对数的底数）.