
科目: 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(Ⅰ)求b的值;
(Ⅱ)判断函数f(x)的单调性;
(Ⅲ)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某测试团队为了研究“饮酒”对“驾车安全”的影响,随机选取![]() 名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试,测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子停下所需要的距离),无酒状态与酒后状态下的试验数据分别列于表
名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试,测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子停下所需要的距离),无酒状态与酒后状态下的试验数据分别列于表![]()
停车距离 |
|
|
|
|
|
频数 | 26 |
|
| 8 | 2 |
表![]()
平均每毫升血液酒精含量 | 10 | 30 | 50 | 70 | 90 | /tr>
平均停车距离 | 30 | 50 | 60 | 70 | 90 |
已知表![]() 数据的中位数估计值为
数据的中位数估计值为![]() ,回答以下问题.
,回答以下问题.
(Ⅰ)求![]() 的值,并估计驾驶员无酒状态下停车距离的平均数;
的值,并估计驾驶员无酒状态下停车距离的平均数;
(Ⅱ)根据最小二乘法,由表![]() 的数据计算
的数据计算![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(Ⅲ)该测试团队认为:驾驶员酒后驾车的平均“停车距离”![]() 大于(Ⅰ)中无酒状态下的停车距离平均数的
大于(Ⅰ)中无酒状态下的停车距离平均数的![]() 倍,则认定驾驶员是“醉驾”.请根据(Ⅱ)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
倍,则认定驾驶员是“醉驾”.请根据(Ⅱ)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?
(附:回归方程![]() 中,
中, 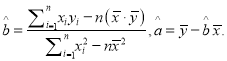 )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)是奇函数,g(x)是偶函数,且在公共定义域{x|x∈R且x≠±1}上满足f(x)+g(x)= ![]() .
.
(1)求f(x)和g(x)的解析式;
(2)设h(x)=f(x)﹣g(x),求h( ![]() );
);
(3)求值:h(2)+h(3)+h(4)+…+h(2016)+h( ![]() )+h(
)+h( ![]() )+h(
)+h( ![]() )+…+h(
)+…+h( ![]() ).
).
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)为定义在R奇函数,当x>0时,f(x)=﹣2x2+4x+1,
(1)求:当x<0时,f(x)的表达式;
(2)用分段函数写出f(x)的表达式;
(3)若函数h(x)=f(x)﹣a恰有三个零点,求a的取值范围(只要求写出结果).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=aln(x+1)﹣x2 , 在(1,2)内任取两个实数x1 , x2(x1≠x2),若不等式 ![]() >1恒成立,则实数a的取值范围为( )
>1恒成立,则实数a的取值范围为( )
A.(28,+∞)
B.[15,+∞)
C.[28,+∞)
D.(15,+∞)
查看答案和解析>>
科目: 来源: 题型:
【题目】有能力互异的3人应聘同一公司,他们按照报名顺序依次接受面试,经理决定“不录用第一个接受面试的人,如果第二个接受面试的人比第一个能力强,就录用第二个人,否则就录用第三个人”,记该公司录用到能力最强的人的概率为p,录用到能力中等的人的概率为q,则(p,q)=( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男 | 女 | 合 计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
合 计 | 60 | 50 | 110 |
根据上述数据能得出的结论是( )
(参考公式与数据:X2= ![]() .当X2>3.841时,有95%的把握说事件A与B有关;当X2>6.635时,有99%的把握说事件A与B有关; 当X2<3.841时认为事件A与B无关.)
.当X2>3.841时,有95%的把握说事件A与B有关;当X2>6.635时,有99%的把握说事件A与B有关; 当X2<3.841时认为事件A与B无关.)
A.有99%的把握认为“爱好该项运动与性别有关”
B.有99%的把握认为“爱好该项运动与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com