
科目: 来源: 题型:
【题目】通过随机询问110名性别不同的行人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如下的列联表:
男 | 女 | 总计 | |
走天桥 | 40 | 20 | 60 |
走斑马线 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由 ![]() ,算得
,算得 ![]()
参照独立性检验附表,得到的正确结论是( )
A.有99%的把握认为“选择过马路的方式与性别有关”
B.有99%的把握认为“选择过马路的方式与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别无关”
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,网格纸上小正方形的边长为![]() ,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )
,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )
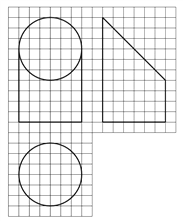
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:

(1)记A表示事件“旧养殖法的箱产量低于50 kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,对这两种养殖方法的优劣进行比较.
附:
P( | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
![]() .
. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=lnx﹣ ![]() .
.
(1)若a>0,试判断f(x)在定义域内的单调性;
(2)若f(x)在[1,e]上的最小值为 ![]() ,求a的值;
,求a的值;
(3)若f(x)>x2在(1,+∞)上恒成立,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解高三年级学生寒假期间的学习情况,某学校抽取了甲、乙两班作为对象,调查这两个班的学生在寒假期间平均每天学习的时间(单位:小时),统计结果绘成频率分布直方图(如图).已知甲、乙两班学生人数相同,甲班学生平均每天学习时间在区间![]() 的有8人.
的有8人.
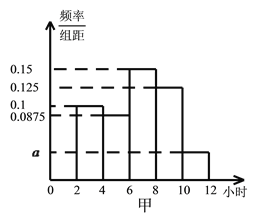

(I)求直方图中![]() 的值及甲班学生平均每天学习时间在区间
的值及甲班学生平均每天学习时间在区间![]() 的人数;
的人数;
(II)从甲、乙两个班平均每天学习时间大于10个小时的学生中任取4人参加测试,设4人中甲班学生的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于定义域为D的函数y=f(x),若同时满足下列条件:
①f(x)在D内单调递增或单调递减;
②存在区间[a,b]D,使f(x)在[a,b]上的值域为[a,b],则把y=f(x),x∈D叫闭函数.
(1)求闭函数y=x3符合条件②的区间[a,b];
(2)判断函数f(x)= ![]() x+
x+ ![]() ,(x>0)是否为闭函数?并说明理由;
,(x>0)是否为闭函数?并说明理由;
(3)已知[a,b]是正整数,且定义在(1,m)的函数y=k﹣ ![]() 是闭函数,求正整数m的最小值,及此时实数k的取值范围.
是闭函数,求正整数m的最小值,及此时实数k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】1927年德国汉堡大学的学生考拉兹提出一个猜想:对于每一个正整数,如果它是奇数,对它乘3再加1,如果它是偶数,对它除以2,这样循环,最终结果都能得到1.该猜想看上去很简单,但有的数学家认为“该猜想任何程度的解决都是现代数学的一大进步,将开辟全新的领域至于如此简单明了的一个命题为什么能够开辟一个全新的领域,这大概与它其中蕴含的奇偶归一思想有关.如图是根据考拉兹猜想设计的一个程序框图,则①处应填写的条件及输出的结果![]() 分别为
分别为
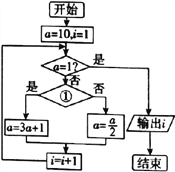
A. ![]() 是偶数?;6 B.
是偶数?;6 B. ![]() 是偶数?;8
是偶数?;8
C. ![]() 是奇数?;5 D.
是奇数?;5 D. ![]() 是奇数?;7
是奇数?;7
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 对一切正整数n,点Pn(n,Sn)都在函数f(x)=x2+2x的图象上,记an与an+1的等差中项为kn .
(1)求数列{an}的通项公式;
(2)若 ![]() ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn;
(3)设集合 ![]() ,等差数列{cn}的任意一项cn∈A∩B,其中c1是A∩B中的最小数,且110<c10<115,求{cn}的通项公式.
,等差数列{cn}的任意一项cn∈A∩B,其中c1是A∩B中的最小数,且110<c10<115,求{cn}的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com