
科目: 来源: 题型:
【题目】已知在直角坐标系 xOy 中,圆锥曲线 C 的参数方程为![]() (
( ![]() 为参数),定点
为参数),定点![]() , F1,F2 是圆锥曲线 C 的左,右焦点.
, F1,F2 是圆锥曲线 C 的左,右焦点.
(1)以原点为极点、 x 轴正半轴为极轴建立极坐标系,求经过点 F1 且平行于直线AF2 的直线 l 的极坐标方程;
(2)在(1)的条件下,设直线 l 与圆锥曲线 C 交于 E,F 两点,求弦 EF 的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明,得到如下列联表:
男 | 女 | 总计 | |
读营养说明 | 16 | 8 | 24 |
不读营养说明 | 4 | 12 | 16 |
总计 | 20 | 20 | 40 |
(1)根据以上列联表进行独立性检验,能否在犯错误的概率不超过0.01的前提下认为性别与是否读营养说明之间有关系?
(2)从被询问的16名不读营养说明的大学生中,随机抽取2名学生,求抽到男生人数![]() 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).
(注:  ,其中
,其中![]() 为样本容量)
为样本容量)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:吨)和年利润
(单位:吨)和年利润![]() (单位:万元)的影响。对近六年的年宣传费
(单位:万元)的影响。对近六年的年宣传费![]() 和年销售量
和年销售量![]() 的数据作了初步统计,得到如下数据:
的数据作了初步统计,得到如下数据:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年宣传费 | 38 | 48 | 58 | 68 | 78 | 88 |
年销售量 | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
经电脑模拟,发现年宣传费![]() (万元)与年销售量
(万元)与年销售量![]() (吨)之间近似满足关系式
(吨)之间近似满足关系式![]() 即
即![]() 。对上述数据作了初步处理,得到相关的值如下表:
。对上述数据作了初步处理,得到相关的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)规定当产品的年销售量![]() (吨)与年宣传费
(吨)与年宣传费![]() (万元)的比值在区间
(万元)的比值在区间![]() 内时认为该年效益良好。现从这6年中任选3年,记其中选到效益良好年的数量为
内时认为该年效益良好。现从这6年中任选3年,记其中选到效益良好年的数量为![]() ,试求随机变量
,试求随机变量![]() 的分布列和期望。(其中
的分布列和期望。(其中![]() 为自然对数的底数,
为自然对数的底数, ![]() )
)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为
查看答案和解析>>
科目: 来源: 题型:
【题目】下列各组函数是同一函数的是( )
①f(x)= ![]() 与g(x)=x
与g(x)=x ![]() ;
;
②f(x)=|x|与g(x)= ![]() ;
;
③f(x)=x0与g(x)= ![]() ;
;
④f(x)=x2﹣2x﹣1与g(t)=t2﹣2t﹣1.
A.①②③
B.①③④
C.②③④
D.①②④
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆锥曲线 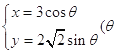 为参数)和定点
为参数)和定点 ![]() F1 , F2是圆锥曲线的左右焦点。
F1 , F2是圆锥曲线的左右焦点。
(1)求经过点F2且垂直于直线AF1的直线l的参数方程;
(2)以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,求直线AF2的极坐标方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】设集合U={x∈N|0<x≤8},S={1,2,4,5},T={3,5,7},则S∩(UT)=( )
A.{1,2,4}
B.{1,2,3,4,5,7}
C.{1,2}
D.{1,2,4,5,6,8}
查看答案和解析>>
科目: 来源: 题型:
【题目】各项均为正数的数列{an}中,a1=1,Sn是数列{an}的前n项和,对任意n∈N* , 有2Sn=2pan2+pan﹣p(p∈R)
(1)求常数p的值;
(2)求数列{an}的通项公式;
(3)记bn= ![]() ,求数列{bn}的前n项和T.
,求数列{bn}的前n项和T.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知在直角坐标系xOy中,圆锥曲线C的参数方程为 ![]() (θ为参数),直线l经过定点P(2,3),倾斜角为
(θ为参数),直线l经过定点P(2,3),倾斜角为 ![]() .
.
(1)写出直线l的参数方程和圆的标准方程;
(2)设直线l与圆相交于A,B两点,求|PA|·|PB|的值
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 和抛物线
和抛物线![]() 交于
交于![]() 两点,且直线
两点,且直线![]() 恰好通过椭圆
恰好通过椭圆![]() 的右焦点
的右焦点![]() ,
,
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)经过![]() 的直线
的直线![]() 和椭圆
和椭圆![]() 交于
交于![]() 两点,交抛物线于
两点,交抛物线于![]() 两点,
两点, ![]() 是抛物线的焦点,是否存在直线
是抛物线的焦点,是否存在直线![]() ,使得
,使得![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程,若不存在,说明理由。
的方程,若不存在,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com