
科目: 来源: 题型:
【题目】在数列{an}中,a1=1,Sn+1=4an+2,则a2013的值为( )
A.3019×22012
B.3019×22013
C.3018×22012
D.无法确定
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,底面△ABC为等腰直角三角形,∠B=90°,D为棱BB1上一点,且平面DA1C⊥平面AA1C1C. 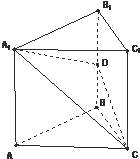
(1)求证:D点为棱BB1的中点;
(2)判断四棱锥A1﹣B1C1CD和C﹣A1ABD的体积是否相等,并证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】“真人秀”热潮在我国愈演愈烈,为了了解学生是否喜欢某“真人秀”节目,在某中学随机调查了110名学生,得到如下列联表:
男 | 女 | 总计 | |
喜欢 | 40 | 20 | 60 |
不喜欢 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由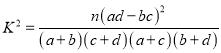 算得
算得![]() .
.
附表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A. 在犯错误的概率不超过![]() 的前提下,认为“喜欢该节目与性别有关”
的前提下,认为“喜欢该节目与性别有关”
B. 在犯错误的概率不超过![]() 的前提下,认为“喜欢该节目与性别无关”
的前提下,认为“喜欢该节目与性别无关”
C. 有![]() 以上的把握认为“喜欢该节目与性别有关”
以上的把握认为“喜欢该节目与性别有关”
D. 有
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点
的右焦点![]() ,过点
,过点![]() 且与坐标轴不垂直的直线与椭圆交于
且与坐标轴不垂直的直线与椭圆交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 经过椭圆的一个顶点时其倾斜角恰好为
经过椭圆的一个顶点时其倾斜角恰好为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,线段
为坐标原点,线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C的中心在原点,离心率等于 ![]() ,它的一个短轴端点恰好是抛物线x2=8
,它的一个短轴端点恰好是抛物线x2=8 ![]() y的焦点.
y的焦点.
(1)求椭圆C的方程;
(2)已知P(2,m)、Q(2,﹣m)(m>0)是椭圆上的两点,A,B是椭圆上位于直线PQ两侧的动点,
①若直线AB的斜率为 ![]() ,求四边形APBQ面积的最大值;
,求四边形APBQ面积的最大值;
②当A、B运动时,满足∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
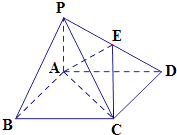
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AP=1,AD=2,E为线段PD上一点,记 ![]() =λ. 当λ=
=λ. 当λ= ![]() 时,二面角D﹣AE﹣C的平面角的余弦值为
时,二面角D﹣AE﹣C的平面角的余弦值为 ![]() .
. 
(1)求AB的长;
(2)当 ![]() 时,求异面直线BP与直线CE所成角的余弦值.
时,求异面直线BP与直线CE所成角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】斜三棱柱ABC﹣A1B1C1中,AA1=AC=BC=2,∠A1AC=∠C1CB=60°,且平面ACC1A1⊥平面BCC1B1 , 则A1B的长度为 . 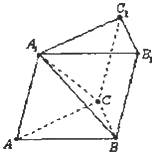
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直三棱柱A1B1C1﹣ABC中,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点. 
(1)求异面直线A1B与C1D所成角的余弦值;
(2)求平面ADC1与ABA1所成二面角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商店计划每天购进某商品若干件,商店每销售1件该商品可获利50元.若供大于求,剩余商品全部退回,则每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利30元.
(Ⅰ)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式;
(Ⅱ)商店记录了50天该商品的日需求量(单位:件),整理得下表:
日需求量n | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 10 | 15 | 10 | 5 |
①假设该店在这50天内每天购进10件该商品,求这50天的日利润(单位:元)的平均数;
②若该店一天购进10件该商品,记“当天的利润在区间![]() ”为事件A,求P(A)的估计值.
”为事件A,求P(A)的估计值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com