【题目】在四棱锥P﹣ABCD中，△PAB为正三角形，四边形ABCD为矩形，平面PAB⊥平面ABCD，AB=2AD，M，N分别为PB，PC中点．
（Ⅰ）求证：MN∥平面PAD；
（Ⅱ）求二面角B﹣AM﹣C的大小；
（Ⅲ）在BC上是否存在点E，使得EN⊥平面AMN？若存在，求 的值；若不存在，请说明理由．

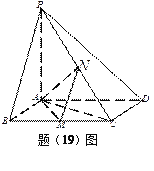
如图，已知四棱锥，底面为菱形，，

, 平面， 分别是的中点。

（1）证明： ；

（2）若为上的动点，与平面所成最大角

的正切值为，求二面角的余弦值。

已知函数（其中a是实数）．

（1）求的单调区间；

（2）若设，且有两个极值点 ，求取值范围．（其中e为自然对数的底数）．

【题目】某机床厂今年初用98万元购进一台数控机床，并立即投入使用，计划第一年维修、保养费用12万元，从第二年开始，每年的维修、保养修费用比上一年增加4万元，该机床使用后，每年的总收入为50万元，设使用x年后数控机床的盈利总额y元．
（1）写出y与x之间的函数关系式；
（2）从第几年开始，该机床开始盈利？
（3）使用若干年后，对机床的处理有两种方案：①当年平均盈利额达到最大值时，以30万元价格处理该机床；②当盈利额达到最大值时，以12万元价格处理该机床．问哪种方案处理较为合理？请说明理由．

【题目】已知函数f（x）=x2+2alnx．
（1）若函数f（x）的图象在（2，f（2））处的切线斜率为1，求实数a的值；
（2）求函数f（x）的单调区间；
（3）若函数 在[1，2]上是减函数，求实数a的取值范围．

【题目】某校举行环保知识竞赛，为了了解本次竞赛成绩情况，从得分不低于50分的试卷中随机抽取100名学生的成绩（得分均为正数，满分100分），进行统计，请根据频率分布表中所提供的数据，解答下列问题：
（Ⅰ）求a、b的值；
（Ⅱ）若从成绩较好的第3、4、5组中，按分层抽样的方法抽取6人参加社区志愿者活动，并从中选出2人做负责人，求2人中至少有1人是第四组的概率．

【题目】已知函数f（x）=ax2+（b﹣8）x﹣a﹣ab，当x∈（﹣3，2）时，f（x）＞0，当x∈（﹣∞，﹣3）∪（2，+∞）时，f（x）＜0．
（1）求f（x）的解析式；
（2）若不等式ax2+bx+c≤0的解集为R，求c的取值范围；
（3）当x＞﹣1时，求y= 的最大值．

【题目】如图，在直三棱柱ABC﹣A1B1C1中，AC⊥BC，点D是AB的中点．求证：
（1）AC⊥BC1；
（2）AC1∥平面B1CD．

【题目】在△ABC中，角A，B，C的对边分别为a，b，c，且b=，cosAsinB+（c﹣sinA）cos（A+C）=0．

（1）求角B的大小；

（2）若△ABC的面积为，求sinA+sinC的值．

【题目】算法如图，若输入m=210，n=117，则输出的n为（ ）
A.2
B.3
C.7
D.11