
科目: 来源: 题型:
【题目】如图,在海岸线![]() 一侧
一侧![]() 处有一个美丽的小岛,某旅游公司为方便游客,在
处有一个美丽的小岛,某旅游公司为方便游客,在![]() 上设立了
上设立了![]() 两个报名点,满足
两个报名点,满足![]() 中任意两点间的距离为
中任意两点间的距离为![]() .公司拟按以下思路运作:先将
.公司拟按以下思路运作:先将![]() 两处游客分别乘车集中到
两处游客分别乘车集中到![]() 之间的中转点
之间的中转点![]() 处(点
处(点![]() 异于
异于![]() 两点),然后乘同一艘轮游轮前往
两点),然后乘同一艘轮游轮前往![]() 岛.据统计,每批游客
岛.据统计,每批游客![]() 处需发车2辆,
处需发车2辆, ![]() 处需发车4辆,每辆汽车每千米耗费
处需发车4辆,每辆汽车每千米耗费![]() 元,游轮每千米耗费
元,游轮每千米耗费![]() 元.(其中
元.(其中![]() 是正常数)设∠
是正常数)设∠![]() ,每批游客从各自报名点到
,每批游客从各自报名点到![]() 岛所需运输成本为
岛所需运输成本为![]() 元.
元.
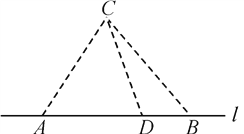
(1) 写出![]() 关于
关于![]() 的函数表达式,并指出
的函数表达式,并指出![]() 的取值范围;
的取值范围;
(2) 问:中转点![]() 距离
距离![]() 处多远时,
处多远时, ![]() 最小?
最小?
查看答案和解析>>
科目: 来源: 题型:
【题目】在单位正方体ABCD﹣A1B1C1D1中,O是B1D1的中点,如图建立空间直角坐标系. 
(1)求证:B1C∥平面ODC1;
(2)求异面直线B1C与OD夹角的余弦值;
(3)求直线B1C到平面ODC1的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】三棱柱ABC﹣A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为AB边中点,且CC1=2AB. 
(1)求证:平面C1CD⊥平面ABC;
(2)求证:AC1∥平面CDB1;
(3)求三棱锥D﹣CAB1的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值;
的距离的最大值;
(Ⅱ)若曲线![]() 上的所有点都在直线
上的所有点都在直线![]() 的下方,求实数
的下方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数 ![]() ,把方程f(x)=x的根按从小到大的顺序排列成一个数列,则该数列的通项公式为( )
,把方程f(x)=x的根按从小到大的顺序排列成一个数列,则该数列的通项公式为( )
A.![]() (n∈N*)
(n∈N*)
B.an=n(n﹣1)(n∈N*)
C.an=n﹣1(n∈N*)
D.an=2n﹣2(n∈N*)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点. 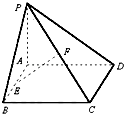
(1)求证:EF∥平面PAD;
(2)求证:EF⊥CD;
(3)若∠PDA=45°,求EF与平面ABCD所成的角的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知命题p:关于x的不等式ax>1,(a>0,a≠1)的解集是{x|x<0},命题q:函数y=lg(x2﹣x+a)的定义域为R,若p∨q为真p∧q为假,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】三棱锥P﹣ABC的四个顶点都在球D的表面上,PA⊥平面ABC,AB⊥BC,PA=3,AB=BC=2,则球O的表面积为( )
A.13π
B.17π
C.52π
D.68π
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数y=x+ ![]() (a>0)在区间
(a>0)在区间 ![]() 上单调递减,在区间
上单调递减,在区间 ![]() 上单调递增;函数
上单调递增;函数 ![]()
(1)请写出函数f(x)=x2+ ![]() (a>0)与函数g(x)=xn+
(a>0)与函数g(x)=xn+ ![]() (a>0,n∈N,n≥3)在(0,+∞)的单调区间(只写结论,不证明);
(a>0,n∈N,n≥3)在(0,+∞)的单调区间(只写结论,不证明);
(2)求函数h(x)的最值;
(3)讨论方程h2(x)﹣3mh(x)+2m2=0(0<m≤30)实根的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com