
科目: 来源: 题型:
【题目】若f(x)是定义在R上的可导函数,且满足(x﹣1)f′(x)≥0,则必有( )
A.f(0)+f(2)<2f(1)
B.f(0)+f(2)>2f(1)
C.f(0)+f(2)≤2f(1)
D.f(0)+f(2)≥2f(1)
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() ,与
,与![]() ,
, ![]() 各有一个交点,当
各有一个交点,当![]() 时,这两个交点间的距离为2,当
时,这两个交点间的距离为2,当![]() ,这两个交点重合.
,这两个交点重合.
(1)分别说明![]() ,
, ![]() 是什么曲线,并求出
是什么曲线,并求出![]() 与
与![]() 的值;
的值;
(2)设当![]() 时,
时, ![]() 与
与![]() ,
, ![]() 的交点分别为
的交点分别为![]() ,当
,当![]() ,
, ![]() 与
与![]() ,
, ![]() 的交点分别为
的交点分别为![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若a,b∈[﹣1,1],a+b≠0时,有 ![]() 成立.
成立.
(1)判断f(x)在[﹣1,1]上的单调性,并证明它;
(2)解不等式f(x2)<f(2x);
(3)若f(x)≤m2﹣2am+1对所有的a∈[﹣1,1]恒成立,求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200.220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图示. (Ⅰ)求直方图中x的值;
(Ⅱ)求月平均用电量的众数和中位数;
(Ⅲ)在月平均用电量为[220,240),[240,260),[260,280)的三组用户中,用分层抽样的方法抽取10户居民,则月平均用电量在[220,240)的用户中应抽取多少户?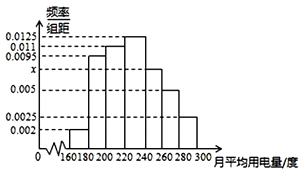
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示.
)的部分图象如图所示. 
(1)求函数的解析式;
(2)设 ![]() π<x<
π<x< ![]() π,且方程f(x)=m有两个不同的实数根,求实数m的取值范围和这两个根的和.
π,且方程f(x)=m有两个不同的实数根,求实数m的取值范围和这两个根的和.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司为了了解一年内的用水情况,抽取了10天的用水量如表所示:
天数 | 1 | 1 | 1 | 2 | 2 | 1 | 2 |
用水量/吨 | 22 | 38 | 40 | 41 | 44 | 50 | 95 |
(Ⅰ)在这10天中,该公司用水量的平均数是多少?每天用水量的中位数是多少?
(Ⅱ)你认为应该用平均数和中位数中的哪一个数来描述该公司每天的用水量?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=2sin (2x+ ![]() ).
).
(1)求函数f(x)的最小正周期及其单调减区间;
(2)用“五点法”画出函数g(x)=f(x),x∈[﹣ ![]() ,
, ![]() ]的图象(完成列表格并作图),由图象研究并写出g(x)的对称轴和对称中心.
]的图象(完成列表格并作图),由图象研究并写出g(x)的对称轴和对称中心.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=ln(1+x),g(x)=xf′(x),x≥0,其中f′(x)是f(x)的导函数.
(1)g1(x)=g(x),gn+1(x)=g(gn(x)),n∈N+ , 求g1(x),g2(x),g3(x),并猜想gn(x)的表达式(不必证明);
(2)若f(x)≥ag(x)恒成立,求实数a的取值范围;
(3)设n∈N+ , 比较g(1)+g(2)+…+g(n)与n﹣f(n)的大小,并用数学归纳法加以证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为梯形,
为梯形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求证:平面![]()
![]() 平面
平面![]() ;
;
(2)设![]() 为
为![]() 上的一点,满足
上的一点,满足![]() ,若直线
,若直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,其中实数
,其中实数![]() 为常数,
为常数,![]() 为自然对数的底数.
为自然对数的底数.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,解关于
时,解关于![]() 的不等式
的不等式![]() ;
;
(3)当![]() 时,如果函数
时,如果函数![]() 不存在极值点,求
不存在极值点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com