
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示.
)的部分图象如图所示. 
(1)求函数的解析式;
(2)设 ![]() π<x<
π<x< ![]() π,且方程f(x)=m有两个不同的实数根,求实数m的取值范围和这两个根的和.
π,且方程f(x)=m有两个不同的实数根,求实数m的取值范围和这两个根的和.
【答案】
(1)解:由函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象,可得A=2,
)的部分图象,可得A=2,
根据 ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() ,求得ω=2.
,求得ω=2.
再根据五点法作图可得2× ![]() +φ=
+φ= ![]() ,∴φ=
,∴φ= ![]() ,f(x)=2sin(2x+
,f(x)=2sin(2x+ ![]() ).
).
(2)解:如图所示,在同一坐标系中画出y=2sin(2x+ ![]() )和直线y=m(m∈R)的图象,
)和直线y=m(m∈R)的图象,
由图可知,当﹣2<m<0或 ![]() <m<2时,直线y=m与曲线有两个不同的交点,即原方程有两个不同的实数根.
<m<2时,直线y=m与曲线有两个不同的交点,即原方程有两个不同的实数根.
∴m的取值范围为:﹣2<m<0或 ![]() <m<2;
<m<2;
当﹣2<m<0时,两根和为 ![]() ; 当
; 当 ![]() <m<2时,两根和为
<m<2时,两根和为 ![]() .
.
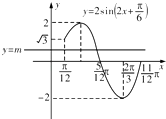
【解析】(1)由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.(2)在同一坐标系中画出y=2sin(2x+ ![]() )和直线y=m(m∈R)的图象,结合正弦函数的图象的特征,数形结合求得实数m的取值范围和这两个根的和.
)和直线y=m(m∈R)的图象,结合正弦函数的图象的特征,数形结合求得实数m的取值范围和这两个根的和.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】假设某种设备使用的年限x(年)与所支出的维修费用y(元)有以下统计资料:

参考数据: ![]() .参考公式:
.参考公式: ![]()

如果由资料知y对x呈线性相关关系.试求:
(1)![]() (2)线性回归方程
(2)线性回归方程![]()
(3)估计使用10年时,维修费用是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的前n项和为Sn , 已知对任意的n∈N+ , 点(n,Sn)均在函数y=bx+r(b>0且b≠1,b,r均为常数的图象上.
(1)求r的值.
(2)当b=2时,记bn=2(log2an+1)(n∈N+),证明:对任意的n∈N+,不等式成立 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中实数
,其中实数![]() 为常数,
为常数,![]() 为自然对数的底数.
为自然对数的底数.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,解关于
时,解关于![]() 的不等式
的不等式![]() ;
;
(3)当![]() 时,如果函数
时,如果函数![]() 不存在极值点,求
不存在极值点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=Asin(ωx+φ)在一个周期内的图象如图,此函数的解析式为( ) 
A.y=2sin(2x+ ![]() )
)
B.y=2sin(2x+ ![]() )??
)??
C.y=2sin( ![]() ﹣
﹣ ![]() )
)
D.y=2sin(2x﹣ ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com