
【题目】已知函数![]() ,
, ![]()
![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若关于![]() 的方程
的方程![]() 有实数根,求实数
有实数根,求实数![]() 的取值范围.
的取值范围.
【答案】(1)单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:
(1)结合函数的解析式可得![]() ,
, ![]() ,结合导函数与原函数的单调性的关系可得函数
,结合导函数与原函数的单调性的关系可得函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)原问题等价于方程![]() 有实数根,构造函数
有实数根,构造函数![]() ,利用导函数研究函数存在零点的充要条件可得:当
,利用导函数研究函数存在零点的充要条件可得:当![]() 时,方程
时,方程![]() 有实数根.
有实数根.
试题解析:
(1)依题意,得![]() ,
, ![]() .
.
令![]() ,即
,即![]() ,解得
,解得![]() ;
;
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
故函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)由题得, ![]()
![]() .
.
依题意,方程![]() 有实数根,
有实数根,
即函数![]() 存在零点,
存在零点,
又![]() ,
,
令![]() ,得
,得![]() .
.
当![]() 时,
时, ![]() ,即函数
,即函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
而![]() ,
, 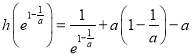
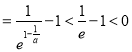 ,
,
所以函数![]() 存在零点;
存在零点;
当![]() 时,
时, ![]() ,
, ![]() 随
随![]() 的变化情况如表:
的变化情况如表:
|
|
|
|
|
|
|
|
|
| 极小值 |
|
所以![]() 为函数
为函数![]() 的极小值,也是最小值.
的极小值,也是最小值.
当![]() ,即
,即![]() 时,函数
时,函数![]() 没有零点;
没有零点;
当![]() ,即
,即![]() 时,注意到
时,注意到![]() ,
, ![]() ,
,
所以函数![]() 存在零点.
存在零点.
综上所述,当![]() 时,方程
时,方程![]() 有实数根.
有实数根.


科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,D是AC的中点,EF∥DB. 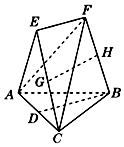
(1)已知AB=BC,AF=CF,求证:AC⊥平面BEF;
(2)已知G、H分别是EC和FB的中点,求证:GH∥平面ABC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示.
)的部分图象如图所示. 
(1)求函数的解析式;
(2)设 ![]() π<x<
π<x< ![]() π,且方程f(x)=m有两个不同的实数根,求实数m的取值范围和这两个根的和.
π,且方程f(x)=m有两个不同的实数根,求实数m的取值范围和这两个根的和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差不为零的等差数列{an}中,a1=1且a1 , a3 , a9成等比数列, (Ⅰ)求数列{an}的通项公式
(Ⅱ)设bn=n2 ![]() 求数列[bn}的前n项和Sn .
求数列[bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)分别求第3,4,5组的频率.
(2)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加广场宣传活动,应从第3,4,5组各抽取多少名志愿者?
(3)在(2)的条件下,我市决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com