（1）若某企业每天由空气污染造成的经济损失S（单位：元）与空气质量指数API（记为ω）的关系式为： S= 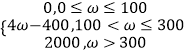，试估计在本年内随机抽取一天，该天经济损失S大于200元且不超过600元的概率；
（2）若本次抽取的样本数据有30天是在供暖季，其中有8天为重度污染，完成下面2×2列联表，并判断能否有95%的把握认为该市本年空气重度污染与供暖有关？ 附：

k2=

【题目】在正方体ABCD﹣A1B1C1D1的各个顶点与各棱的中点共20个点中，任取2点连成直线，在这些直线中任取一条，它与对角线BD1垂直的概率为（ ）
A.
B.
C.
D.

【题目】[ ]表示不超过 的最大整数．若 S1=[ ]+[ ]+[ ]=3，
S2=[ ]+[ ]+[ ]+[ ]+[ ]=10，
S3=[ ]+[ ]+[ ]+[ ]+[ ]+[ ]+[ ]=21，
…，
则Sn=（ ）
A.n（n+2）
B.n（n+3）
C.（n+1）2﹣1
D.n（2n+1）

【题目】设函数．

（）求数的最小正周期和对称轴方程．

（）锐角的三个顶点， ， 所对边分别为， ， ，若， ， ，求及边．

（）若中， ，求的取值范围．

【题目】已知函数 是奇函数，f（x）=lg（10x+1）+bx是偶函数．
（1）求a和b的值．
（2）说明函数g（x）的单调性；若对任意的t∈[0，+∞），不等式g（t2﹣2t）+g（2t2﹣k）＞0恒成立，求实数k的取值范围．
（3）设 ，若存在x∈（﹣∞，1]，使不等式g（x）＞h[lg（10a+9）]成立，求实数a的取值范围．

【题目】将一枚骰子投掷两次，所得向上点数分别为m和n，则函数y=mx2﹣nx+1在[1，+∞）上为增函数的概率是（ ）
A.
B.
C.
D.

【题目】已知直线l：ax﹣y+1=0与x轴，y轴分别交于点A，B．
（1）若a＞0，点M（1，﹣1），点N（1，4），且以MN为直径的圆过点A，求以AN为直径的圆的方程；
（2）以线段AB为边在第一象限作等边三角形ABC，若a=﹣ ，且点P（m， ）（m＞0）满足△ABC与△ABP的面积相等，求m的值．

【题目】设函数f（x）=lnx+ ，m∈R，若对任意b＞a＞0， ＜1恒成立，则m的取值范围为 ．

【题目】某电影院共有1000个座位，票价不分等次，根据影院的经营经验，当每张票价不超过10元时，票可全售出；当每张票价高于10元时，每提高1元，将有30张票不能售出，为了获得更好的收益，需给影院定一个合适的票价，需符合的基本条件是：①为了方便找零和算账，票价定为1元的整数倍；②电影院放一场电影的成本费用支出为5750元，票房的收入必须高于成本支出，用x（元）表示每张票价，用y（元）表示该影院放映一场的净收入（除去成本费用支出后的收入），问：
（1）把y表示为x的函数，并求其定义域；
（2）试问在符合基本条件的前提下，票价定为多少时，放映一场的净收人最多？

【题目】已知函数在区间上有最大值4和最小值1.设.

（1）求的值；

（2）若不等式在上有解，求实数的取值范围；

（3）若有三个不同的实数解，求实数的取值范围.