【题目】为得到函数y=cos（2x+ ）的图象，只需将函数y=cos2x的图象（ ）
A.向左平移 个长度单位
B.向右平移 个长度单位
C.向左平移 个长度单位
D.向右平移 个长度单位

【题目】已知函数f（x）=lg（x2+tx+2）（t为常数，且﹣2 ＜t＜2 ）．
（1）当x∈[0，2]时，求函数f（x）的最小值（用t表示）；
（2）是否存在不同的实数a，b，使得f（a）=lga，f（b）=lgb，并且a，b∈（0，2）．若存在，求出实数t的取值范围；若不存在，请说明理由．

【题目】设，.

（1）令，求的单调区间；

（2）当时，证明.

【题目】已知向量 =（sinx，2cosx）， =（5 cosx，cosx），函数f（x）= +| |2﹣ ．
（1）求函数f（x）的最小正周期；
（2）若x∈（ ， ）时，f（x）=﹣3，求cos2x的值；
（3）若cosx≥ ，x∈（﹣ ， ），且f（x）=m有且仅有一个实根，求实数m的取值范围．

【题目】函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜ ）的图象与y轴的交点为（0， ），它的一个对称中心是M（ ，0），点M与最近的一条对称轴的距离是 ．
（1）求此函数的解析式；
（2）求此函数取得最大值时x的取值集合；
（3）当x∈（0，π）时，求此函数的单调递增区间．

【题目】已知椭圆 + =1（a＞b＞0）的离心率为 ，且过点（ ， ）．
（1）求椭圆方程；
（2）设不过原点O的直线l：y=kx+m（k≠0），与该椭圆交于P、Q两点，直线OP、OQ的斜率依次为k1、k2 ， 满足4k=k1+k2 ， 试问：当k变化时，m2是否为定值？若是，求出此定值，并证明你的结论；若不是，请说明理由．

【题目】已知直线l经过点P（2，﹣1），且在两坐标轴上的截距之和为2，圆M的圆心在直线2x+y=0上，且与直线l相切于点P．
（1）求直线l的方程；
（2）求圆M的方程；
（3）求圆M在y轴上截得的弦长．

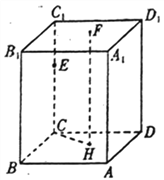
【题目】如图所示，直平行六面体中，为棱上任意一点，为底面（除外）上一点，已知在底面上的射影为，若再增加一个条件，就能得到，现给出以下条件：

①；②在上；③平面；④直线和在平面的射影为同一条直线．其中一定能成为增加条件的是__________．（把你认为正确的都填上）

【题目】在四边形ABCD中， =（2，﹣2）， =（x，y）， =（1， ）．
（1）若 ∥ ，求x，y之间的关系式；
（2）满足（1）的同时又有 ⊥ ，求x，y的值以及四边形ABCD的面积．

【题目】现有一块大型的广告宣传版面，其形状如图所示的直角梯形．某厂家因产品宣传的需要，拟出资规划出一块区域（图中阴影部分）为产品做广告，形状为直角梯形（点在曲线段上，点在线段上）．已知，，其中曲线段是以为顶点，为对称轴的抛物线的一部分．

（1）求线段，线段，曲线段所围成区域的面积；

（2）求厂家广告区域的最大面积．