【题目】已知函数f（x）是定义在R上的偶函数，且当x≥0时，f（x）=x|x﹣2|．若关于x的方程f2（x）+af（x）+b=0（a，b∈R）恰有10个不同实数解，则a的取值范围为（ ）
A.（0，2）
B.（﹣2，0）
C.（1，2）
D.（﹣2，﹣1）

【题目】下面有命题： ①y=|sinx﹣ |的周期是π；
②y=sinx+sin|x|的值域是[0，2]；
③方程cosx=lgx有三解；
④ω为正实数，y=2sinωx在 上递增，那么ω的取值范围是 ；
⑤在y=3sin（2x+ ）中，若f（x1）=f（x2）=0，则x1﹣x2必为π的整数倍；
⑥若A、B是锐角△ABC的两个内角，则点P（cosB﹣sinA，sinB﹣cosA在第二象限；
⑦在△ABC中，若 ，则△ABC钝角三角形．其中真命题个数为（ ）
A.2
B.3
C.4
D.5

【题目】已知数列的前项和为，满足，．数列满足，，且．

（1）求数列和的通项公式；

（2）若，数列的前项和为，对任意的，都有，求实数的取值范围；

（3）是否存在正整数，，使，，（）成等差数列，若存在，求出所有满足条件的，，若不存在，请说明理由．

【题目】已知函数f（x）=3x+x，g（x）=x3+x，h（x）=log3x+x的零点依次为a，b，c，则（ ）
A.c＜b＜a
B.a＜b＜c
C.c＜a＜b
D.b＜a＜c

【题目】要得到函数 的图象，只需要将函数y=sin3x的图象（ ）m．
A.向右平移 个单位
B.向左平移 个单位
C.向右平移 个单位
D.向左平移 个单位

【题目】某园林公司准备绿化一块半径为200米，圆心角为 的扇形空地（如图的扇形OPQ区域），扇形的内接矩形ABCD为一水池，其余的地方种花，若∠COP=α，矩形ABCD的面积为S（单位：平方米）．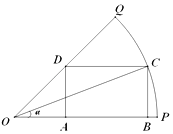
（1）试将S表示为关于α的函数，求出该函数的表达式；
（2）角α取何值时，水池的面积 S最大，并求出这个最大面积．

【题目】某同学用“五点法”画函数 在区间[﹣ ， ]上的图象时，列表并填入了部分数据，如表：

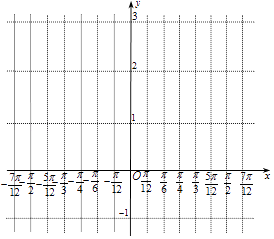
（1）请将上表数据补充完整，并在给出的直角坐标系中，画出f（x）在区间[﹣ ， ]上的图象；
（2）求f（x）的最小值及取最小值时x的集合；
（3）求f（x）在 时的值域．

【题目】某同学在上学路上要经过、、三个带有红绿灯的路口.已知他在、、三个路口遇到红灯的概率依次是、、，遇到红灯时停留的时间依次是秒、秒、秒，且在各路口是否遇到红灯是相互独立的.

（1）求这名同学在上学路上在第三个路口首次遇到红灯的概率；，

（2）求这名同学在上学路上因遇到红灯停留的总时间.