
【题目】已知函数f(x)是定义在R上的偶函数,且当x≥0时,f(x)=x|x﹣2|.若关于x的方程f2(x)+af(x)+b=0(a,b∈R)恰有10个不同实数解,则a的取值范围为( )
A.(0,2)
B.(﹣2,0)
C.(1,2)
D.(﹣2,﹣1)
【答案】D
【解析】解:设x<0,则﹣x>0,满足表达式f(x)=x|x﹣2|. ∴f(﹣x)=﹣x|﹣x﹣2|=﹣x|x+2|,
又∵f(x)为偶函数,∴f(﹣x)=f(x),
∴f(x)=﹣x|x+2|,
故当x<0时,f(x)=﹣x|x+2|.
则f(x)= ![]() ,
,
作出f(x)的图象如图:
设t=f(x),
由图象知,当t>1时,t=f(x)有两个根,
当t=1时,t=f(x)有四个根,
当0<t<1时,t=f(x)有六两个根,
当t=0时,t=f(x)有三个根,
当t<0时,t=f(x)有0个根,
则方程[f(x)]2+af(x)+b=0等价为t2+at+b=0,
若方程[f(x)]2+af(x)+b=0(a∈R)恰好有1个不同实数解,
等价为方程t2+at+b=0有两不同的根,
且0<t1<1,t2=1,
则t1+t2=﹣a,
即1<t1+t2<2,
则1<﹣a<2,
即﹣2<a<﹣1,
则a的取值范围为(﹣2,﹣1),
故选D.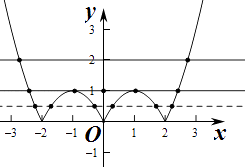
【考点精析】利用函数奇偶性的性质对题目进行判断即可得到答案,需要熟知在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】定义在R上的偶函致y=f(x),恒有f(x+4)=f(x)﹣f(﹣2)成立,且f(0)=1,当0≤x1<x2≤2时, ![]() <0,则方程f(x)﹣lg|x|=0的根的个数为( )
<0,则方程f(x)﹣lg|x|=0的根的个数为( )
A.12
B.10
C.6
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() ,设直线
,设直线![]() 的斜率是
的斜率是![]() ,且
,且![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆的标准方程.
(Ⅱ)若直线![]() 在
在![]() 轴上的截距是
轴上的截距是![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
(Ⅲ)以![]() 为底作等腰三角形,顶点为
为底作等腰三角形,顶点为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数.
上的奇函数.
(1)当![]() 时,
时, ![]() ,若当
,若当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的最小值;
的最小值;
(2)若![]() 的图像关于
的图像关于![]() 对称,且
对称,且![]() 时,
时, ![]() ,求当
,求当![]() 时,
时, ![]() 的解析式;
的解析式;
(3)当![]() 时,
时, ![]() .若对任意的
.若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某园林公司准备绿化一块半径为200米,圆心角为 ![]() 的扇形空地(如图的扇形OPQ区域),扇形的内接矩形ABCD为一水池,其余的地方种花,若∠COP=α,矩形ABCD的面积为S(单位:平方米).
的扇形空地(如图的扇形OPQ区域),扇形的内接矩形ABCD为一水池,其余的地方种花,若∠COP=α,矩形ABCD的面积为S(单位:平方米). 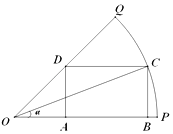
(1)试将S表示为关于α的函数,求出该函数的表达式;
(2)角α取何值时,水池的面积 S最大,并求出这个最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知任意角θ以x轴非负半轴为始边,若终边经过点P(x0 , y0),且|OP|=r(r>0),定义sicosθ= ![]() ,称“sicosθ”为“正余弦函数”.对于正余弦函数y=sicosx,有同学得到如下结论: ①该函数是偶函数;
,称“sicosθ”为“正余弦函数”.对于正余弦函数y=sicosx,有同学得到如下结论: ①该函数是偶函数;
②该函数的一个对称中心是( ![]() ,0);
,0);
③该函数的单调递减区间是[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ],k∈Z.
],k∈Z.
④该函数的图象与直线y= ![]() 没有公共点;
没有公共点;
以上结论中,所有正确的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,
, ![]() ,
, ![]() ;
;
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,且
,且![]() 是单调递增数列,求实数
是单调递增数列,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,
, ![]() ,对于任意给定的正整数
,对于任意给定的正整数![]() ,是否存在正整数
,是否存在正整数![]() 、
、![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 、
、![]() 的值(只要写出一组即可);若不存在,请说明理由;
的值(只要写出一组即可);若不存在,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2为椭圆 ![]() 的左、右焦点,F2在以
的左、右焦点,F2在以 ![]() 为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.
为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.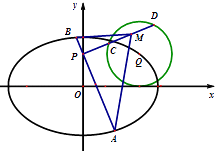
(1)求椭圆C1的方程;
(2)过点P(0,1)的直线l1交椭圆C1于A,B两点,过P与l1垂直的直线l2交圆C2于C,D两点,M为线段CD中点,求△MAB面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com