【题目】已知圆C1：x2+y2=4与圆C2：（x﹣1）2+（y﹣3）2=4，过动点P（a，b）分别作圆C1、圆C2的切线PM，PN，（M，N分别为切点），若|PM|=|PN|，则a2+b2﹣6a﹣4b+13的最小值是（ ）
A.5
B.
C.
D.

【题目】若三棱锥的三条侧棱两两垂直，侧棱长分别为1， ，2，且它的四个顶点在同一球面上，则此球的体积为（ ）
A.
B.
C.
D.8π

【题目】在平面直角坐标系中，直线的参数方程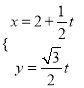（为参数），以坐标原点为极点， 轴正半轴为极轴建立极坐标系，曲线的极坐标方程为： ．

（1）把直线的参数方程化为极坐标方程，把曲线的极坐标方程化为普通方程；

（2）求直线与曲线交点的极坐标（≥0，0≤）．

【题目】已知直线l1：2x﹣y+1=0，直线l2与l1关于直线y=﹣x对称，则直线l2的方程为（ ）
A.x﹣2y+1=0
B.x+2y+1=0
C.x﹣2y﹣1=0
D.x+2y﹣1=0

【题目】已知对任意x∈R，恒有f（﹣x）=﹣f（x），g（﹣x）=g（x），且当x＞0时，f′（x）＞0，g′（x）＞0，则当x＜0时有（ ）
A.f′（x）＞0，g′（x）＞0
B.f′（x）＞0，g′（x）＜0
C.f′（x）＜0，g′（x）＞0
D.f′（x）＜0，g′（x）＜0

【题目】已知二次函数g（x）=mx2﹣2mx+n+1（m＞0）在区间[0，3]上有最大值4，最小值0．
（1）求函数g（x）的解析式；
（2）设f（x）= ．若f（2x）﹣k2x≤0在x∈[﹣3，3]时恒成立，求k的取值范围．

【题目】如图，四边形ABCD为矩形，DA⊥平面ABE，AE=EB=BC=2，BF⊥平面ACE于点F，且点F在CE上．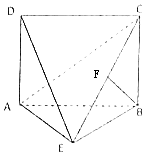
（1）求证：AE⊥BE；
（2）求三棱锥C﹣ADE的体积．

【题目】已知圆C：（x﹣2）2+y2=9，直线l：x+y=0．
（1）求过圆C的圆心且与直线l垂直的直线n的方程；
（2）求与圆C相切，且与直线l平行的直线m的方程．

【题目】已知定义域为R的函数f（x）= 是奇函数，f（1）=﹣ ．
（1）求a，b的值；
（2）判断函数f（x）的单调性，并用定义证明．

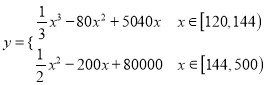【题目】某公司为了变废为宝，节约资源，新上了一个从生活垃圾中提炼生物柴油的项目．经测算，该项目月处理成本（元）与月处理量（吨）之间的函数关系可以近似地表示为： ，且每处理一吨生活垃圾，可得到能利用的生物柴油价值为元，若该项目不获利，政府将给予补贴．

（1）当时，判断该项目能否获利？如果获利，求出最大利润；如果不获利，则政府每月至少需要补贴多少元才能使该项目不亏损？

（2）该项目每月处理量为多少吨时，才能使每吨的平均处理成本最低？