
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且椭圆上一点
,且椭圆上一点![]() 与椭圆左右两个焦点构成的三角形周长为
与椭圆左右两个焦点构成的三角形周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
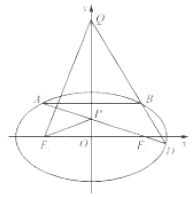
(2)如图,设点![]() 为椭圆上任意一点,直线
为椭圆上任意一点,直线![]() 和椭圆
和椭圆![]() 交于
交于![]() 两点,且直线
两点,且直线![]() 与
与![]() 轴分别交于
轴分别交于![]() 两点,求证:
两点,求证: ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】函数f(x)=Asin(ωx﹣ ![]() )(A>0,ω>0)的最大值为2,其图象相邻两条对称轴之间的距离为
)(A>0,ω>0)的最大值为2,其图象相邻两条对称轴之间的距离为 ![]() . (Ⅰ)求函数f(x)的最小正周期及解析式;
. (Ⅰ)求函数f(x)的最小正周期及解析式;
(Ⅱ)求函数f(x)的单调减区间.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,锐角△ABC中, ![]() =
= ![]() ,
, ![]() =
= ![]() ,点M为BC的中点. (Ⅰ)试用
,点M为BC的中点. (Ⅰ)试用 ![]() ,
, ![]() 表示
表示 ![]() ;
;
(Ⅱ)若| ![]() |=5,|
|=5,| ![]() |=3,sin∠BAC=
|=3,sin∠BAC= ![]() ,求中线AM的长.
,求中线AM的长.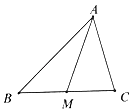
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=2cos2x+2 ![]() sinxcosx+a,且当
sinxcosx+a,且当 ![]() 时,f(x)的最小值为2.
时,f(x)的最小值为2.
(1)求a的值,并求f(x)的单调增区间;
(2)将函数y=f(x)的图象上各点的纵坐标保持不变,横坐标缩短到原来的 ![]() ,再把所得图象向右平移
,再把所得图象向右平移 ![]() 个单位,得到函数y=g(x),求方程g(x)=2在区间
个单位,得到函数y=g(x),求方程g(x)=2在区间 ![]() 上的所有根之和.
上的所有根之和.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=ax+x2﹣xlna(a>0且a≠1)
(1)求函数f(x)单调递增区间;
(2)若存在x1 , x2∈[﹣1,1],使得|f(x1)﹣f(x2)|≥e﹣1(e是自然对数的底数),求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】漳州市“网约车”的现行计价标准是:路程在2km以内(含2km)按起步价8元收取,超过2km后的路程按1.9元/km收取,但超过10km后的路程需加收50%的返空费(即单价为1.9×(1+50%)=2.85元).
(1)将某乘客搭乘一次“网约车”的费用f(x)(单位:元)表示为行程x(0<x≤60,单位:km)的分段函数;
(2)某乘客的行程为16km,他准备先乘一辆“网约车”行驶8km后,再换乘另一辆“网约车”完成余下行程,请问:他这样做是否比只乘一辆“网约车”完成全部行程更省钱?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设甲、乙、丙面试合格的概率分别是 ![]() ,
, ![]() ,
, ![]() ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(1)至少有1人面试合格的概率;
(2)签约人数ξ的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名高三学生的课外体育锻炼平均每天运动的时间进行调查,如表:(平均每天锻炼的时间单位:分钟)
平均每天锻炼 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) |
总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
将学生日均课外课外体育运动时间在[40,60)上的学生评价为“课外体育达标”.
(1)请根据上述表格中的统计数据填写下面2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
课外体育不达标 | 课外体育达标 | 合计 | |
男 | |||
女 | 20 | 110 | |
合计 |
(2)将上述调查所得到的频率视为概率.现在从该校高三学生中,抽取3名学生,记被抽取的3名学生中的“课外体育达标”学生人数为X,若每次抽取的结果是相互独立的,求X的数学期望和方差.
参考公式: ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 的顶点在原点,焦点在
的顶点在原点,焦点在![]() 轴上,且抛物线上有一点
轴上,且抛物线上有一点![]() 到焦点的距离为5.
到焦点的距离为5.
(1)求该抛物线![]() 的方程;
的方程;
(2)已知抛物线上一点![]() ,过点
,过点![]() 作抛物线的两条弦
作抛物线的两条弦![]() 和
和![]() ,且
,且![]() ,判断直线
,判断直线![]() 是否过定点?并说明理由.
是否过定点?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)当 ![]() 时,求函数f(x)的取值范围;
时,求函数f(x)的取值范围;
(2)将f(x)的图象向左平移 ![]() 个单位得到函数g(x)的图象,求g(x)的单调递增区间.
个单位得到函数g(x)的图象,求g(x)的单调递增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com