
科目: 来源: 题型:
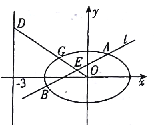
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,如图所示,斜率为
,如图所示,斜率为![]() 且不过原点的直线
且不过原点的直线![]() 交椭圆
交椭圆![]() 于两点
于两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,射线
,射线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求![]() 的最小值;
的最小值;
(2)若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列四组函数中,表示同一函数的是( )
A.f(x)=|x|,g(x)= ![]()
B.f(x)=lg x2 , g(x)=2lg x
C.f(x)= ![]() ,g(x)=x+1
,g(x)=x+1
D.f(x)= ![]() ?
? ![]() ,g(x)=
,g(x)= ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(a,0)(a>0),B(0,a),C(﹣4,0),D(0,4)设△AOB的外接圆圆心为E. 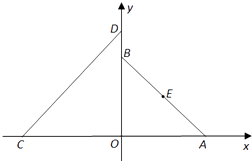
(1)若⊙E与直线CD相切,求实数a的值;
(2)设点P在圆E上,使△PCD的面积等于12的点P有且只有三个,试问这样的⊙E是否存在,若存在,求出⊙E的标准方程;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,平面PAC⊥平面ABC,PA⊥AC,AB⊥BC.设D,E分别为PA,AC中点.
(Ⅰ)求证:DE∥平面PBC;
(Ⅱ)求证:BC⊥平面PAB;
(Ⅲ)试问在线段AB上是否存在点F,使得过三点 D,E,F的平面内的任一条直线都与平面PBC平行?若存在,指出点F的位置并证明;若不存在,请说明理由.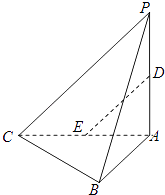
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆C:x2+y2+2x﹣4y+1=0,O为坐标原点,动点P在圆C外,过P作圆C的切线,设切点为M.
(1)若点P运动到(1,3)处,求此时切线l的方程;
(2)求满足条件|PM|=|PO|的点P的轨迹方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥S﹣ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( ) 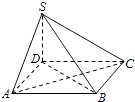
A.AC⊥SB
B.AB∥平面SCD
C.SA与平面SBD所成的角等于SC与平面SBD所成的角
D.AB与SC所成的角等于DC与SA所成的角
查看答案和解析>>
科目: 来源: 题型:
【题目】小明同学在寒假社会实践活动中,对白天平均气温与某家奶茶店的![]() 品牌饮料销量之间的关系进行了分析研究,他分别记录了1月11日至1月15日的白天气温
品牌饮料销量之间的关系进行了分析研究,他分别记录了1月11日至1月15日的白天气温![]() (
(![]() )与该奶茶店的
)与该奶茶店的![]() 品牌饮料销量
品牌饮料销量![]() (杯),得到如表数据:
(杯),得到如表数据:
日期 | 1月11号 | 1月12号 | 1月13号 | 1月14号 | 1月15号 |
平均气温 | 9 | 10 | 12 | 11 | 8 |
销量 | 23 | 25 | 30 | 26 | 21 |
(1)若先从这五组数据中抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出![]() 关于
关于![]() 的线性回归方程式
的线性回归方程式![]() ;
;
(3)根据(2)所得的线性回归方程,若天气预报1月16号的白天平均气温为![]() ,请预测该奶茶店这种饮料的销量.
,请预测该奶茶店这种饮料的销量.
(参考公式: ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com