
科目: 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的部分图象如图所示.
)的部分图象如图所示.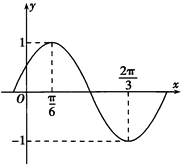
(1)求函数f(x)的解析式,并写出f(x)的单调减区间;
(2)已知△ABC的内角分别是A,B,C,A为锐角,且f ![]() ,求cosA的值.
,求cosA的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设平面向量 ![]() =(cosx,sinx),
=(cosx,sinx), ![]() =(cosx+2
=(cosx+2 ![]() ,sinx),
,sinx), ![]() =(sinα,cosα),x∈R.
=(sinα,cosα),x∈R.
(1)若 ![]() ,求cos(2x+2α)的值;
,求cos(2x+2α)的值;
(2)若α=0,求函数f(x)= ![]() 的最大值,并求出相应的x值.
的最大值,并求出相应的x值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知一组数据x1 , x2 , x3 , x4 , x5的平均数是2,方差是 ![]() ,那么另一组数据2x1﹣1,2x2﹣1,2x3﹣1,2x4﹣1,2x5﹣1的平均数,方差分别是( )
,那么另一组数据2x1﹣1,2x2﹣1,2x3﹣1,2x4﹣1,2x5﹣1的平均数,方差分别是( )
A.3, ![]()
B.3, ![]()
C.4, ![]()
D.4, ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,已知椭圆C: ![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ![]() ,左顶点为A(﹣4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.
,左顶点为A(﹣4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E. 
(1)求椭圆C的方程;
(2)已知P为AD的中点,是否存在定点Q,对于任意的k(k≠0)都有OP⊥EQ,若存在,求出点Q的坐标;若不存在说明理由;
(3)若过O点作直线l的平行线交椭圆C于点M,求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某综艺频道举行某个水上娱乐游戏,如图,固定在水面上点![]() 处的某种设备产生水波圈,水波圈生产
处的某种设备产生水波圈,水波圈生产![]() 秒时的半径
秒时的半径![]() (单位:
(单位: ![]() )满足
)满足![]() ;
; ![]() 是铺设在水面上的浮桥,浮桥的宽度忽略不计,浮桥两端
是铺设在水面上的浮桥,浮桥的宽度忽略不计,浮桥两端![]() 固定在水岸边.游戏规定:当点
固定在水岸边.游戏规定:当点![]() 处刚产生水波圈时,游戏参与者(视为一个点)与此同时从浮桥的
处刚产生水波圈时,游戏参与者(视为一个点)与此同时从浮桥的![]() 端跑向
端跑向![]() 端;若该参与者通过浮桥
端;若该参与者通过浮桥![]() 的过程中,从点
的过程中,从点![]() 处发出的水波圈始终没能到达此人跑动时的位置,则认定该参与者在这个游戏中过关;否则认定在这个游戏中不过关,已知
处发出的水波圈始终没能到达此人跑动时的位置,则认定该参与者在这个游戏中过关;否则认定在这个游戏中不过关,已知![]() ,
, ![]() ,浮桥
,浮桥![]() 的某个桥墩处点
的某个桥墩处点![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,且
,且![]() ,若某游戏参与者能以
,若某游戏参与者能以![]() 的速度从浮桥
的速度从浮桥![]() 端匀速跑到
端匀速跑到![]() 端.
端.
(1)求该游戏参与者从浮桥![]() 端跑到
端跑到![]() 端所需的时间?
端所需的时间?
(2)问该游戏参与者能否在这个游戏中过关?请说明理由.
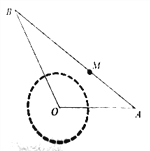
查看答案和解析>>
科目: 来源: 题型:
【题目】南京市江北新区计划在一个竖直长度为20米的瀑布![]() 正前方修建一座观光电梯
正前方修建一座观光电梯![]() 。如图所示,瀑布底部
。如图所示,瀑布底部![]() 距离水平地面的高度
距离水平地面的高度![]() 为60米,电梯上设有一个安全拍照口
为60米,电梯上设有一个安全拍照口![]() ,
, ![]() 上升的最大高度为60米。设
上升的最大高度为60米。设![]() 距离水平地面的高度为
距离水平地面的高度为![]() 米,
米, ![]() 处拍照瀑布的视角
处拍照瀑布的视角![]() 为
为![]() 。摄影爱好者发现,要使照片清晰,视角
。摄影爱好者发现,要使照片清晰,视角![]() 不能小于
不能小于![]() 。
。
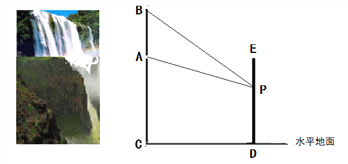
(1)当![]() 米时,视角
米时,视角![]() 恰好为
恰好为![]() ,求电梯和山脚的水平距离
,求电梯和山脚的水平距离![]() 。
。
(2)要使电梯拍照口![]() 的高度
的高度![]() 在52米及以上时,拍出的照片均清晰,请求出电梯和山脚的水平距离
在52米及以上时,拍出的照片均清晰,请求出电梯和山脚的水平距离![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目: 来源: 题型:
【题目】设两个非零向量 ![]() 与
与 ![]() 不共线.
不共线.
(1)若 ![]() =
= ![]() +
+ ![]() ,
, ![]() =2
=2 ![]() +8
+8 ![]() ,
, ![]() =3(
=3( ![]() ﹣
﹣ ![]() ).求证:A,B,D三点共线;
).求证:A,B,D三点共线;
(2)试确定实数k,使k ![]() +
+ ![]() 和
和 ![]() +k
+k ![]() 共线.
共线.
查看答案和解析>>
科目: 来源: 题型:
【题目】给出下列命题:
①函数 ![]() 是奇函数;
是奇函数;
②存在实数α,使得sinα+cosα= ![]() ;
;
③若α,β是第一象限角且α<β,则tanα<tanβ;
④ ![]() 是函数
是函数 ![]() 的一条对称轴方程;
的一条对称轴方程;
⑤函数 ![]() 的图象关于点
的图象关于点 ![]() 成中心对称图形.
成中心对称图形.
其中命题正确的是(填序号).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆M:x2+(y﹣4)2=4,点P是直线l:x﹣2y=0上的一动点,过点P作圆M的切线PA,PB,切点为A,B.
(1)当切线PA的长度为 ![]() 时,求点P的坐标;
时,求点P的坐标;
(2)若△PAM的外接圆为圆N,试问:当P在直线l上运动时,圆N是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由.
(3)求线段AB长度的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com