【题目】如图1所示，在边长为24的正方形中，点在边上，且， ，作分别交、于点，作分别交于点，将该正方形沿折叠，使得与重合，构成如图2所示的三棱柱.

（1）求证： 平面；

（2）求多面体的体积.

【题目】已知圆C的方程为（x﹣1）2+（y﹣2）2=4． （Ⅰ）求过点M（3，1）的圆C的切线方程；
（Ⅱ）判断直线ax﹣y+3=0与圆C的位置关系．

【题目】图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入的a，b，i的值分别为8，10，0，则输出的a和i和值分别为（ ）
A.2，5
B.2，4
C.0，4
D.0，5

【题目】已知棱长为1的正方体ABCD﹣A1B1C1D1中，E，F分别是棱B1C1 ， C1D1的中点． （Ⅰ）求AD1与EF所成角的大小；
（Ⅱ）求AF与平面BEB1所成角的余弦值．

【题目】圆心在y轴上，半径为1，且过点（1，2）的圆的方程为（ ）
A.x2+（y﹣2）2=1
B.x2+（y+2）2=1
C.（x﹣1）2+（y﹣3）2=1
D.x2+（y﹣3）2=1

【题目】已知函数f（x）=Asin（ωx+φ），x∈R（其中 ）的图象与x轴的交点中，相邻两个交点之间的距离为 ，且图象上一个最低点为 ． （Ⅰ）求f（x）的解析式；
（Ⅱ）当 ，求f（x）的值域．

【题目】已知梯形CEPD如图（1）所示，其中PD=8，CE=6，A为线段PD的中点，四边形ABCD为正方形，现沿AB进行折叠，使得平面PABE⊥平面ABCD，得到如图（2）所示的几何体．已知当点F满足 = （0＜λ＜1）时，平面DEF⊥平面PCE，则λ的值为（ ）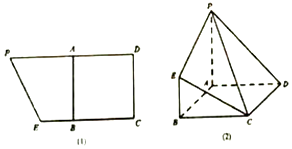
A.
B.
C.
D.

【题目】已知双曲线C1： =1（a＞b＞0）的左、右焦点分别为F1 ， F2 ， 点M在双曲线C1的一条渐近线上，且OM⊥MF2 ， 若△OMF2的面积为16，且双曲线C1与双曲线C2： =1的离心率相同，则双曲线C1的实轴长为（ ）
A.32
B.16
C.8
D.4

【题目】某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜ ）在某一个周期内的图象时，列表并填入了部分数据，如表：

（1）请将上表数据补充完整，填写在相应位置，并直接写出函数f（x）的解析式；
（2）将y=f（x）图象上所有点向左平行移动θ（θ＞0）个单位长度，得到y=g（x）的图象．若y=g（x）图象的一个对称中心为（ ，0），求θ的最小值．

【题目】已知函数y=acosx+b的最大值为1，最小值为﹣3，试确定 的递增区间．