
科目: 来源: 题型:
【题目】在直角坐标系xOy中,直线C1的参数方程为 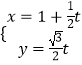 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ2(1+2sin2θ)=3.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ2(1+2sin2θ)=3.
(Ⅰ)写出C1的普通方程和C2的直角坐标方程;
(Ⅱ)直线C1与曲线C2相交于A,B两点,点M(1,0),求||MA|﹣|MB||.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左、右焦点分别为F1、F2 , |F1F2|=4,P是双曲线右支上一点,直线PF2交y轴于点A,△APF1的内切圆切边PF1于点Q,若|PQ|=1,则双曲线的离心率为 .
=1(a>0,b>0)的左、右焦点分别为F1、F2 , |F1F2|=4,P是双曲线右支上一点,直线PF2交y轴于点A,△APF1的内切圆切边PF1于点Q,若|PQ|=1,则双曲线的离心率为 . 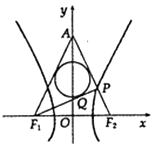
查看答案和解析>>
科目: 来源: 题型:
【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度![]() (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度![]() (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当![]() 不超过4(尾/立方米)时,
不超过4(尾/立方米)时,![]() 的值为
的值为![]() (千克/年);当
(千克/年);当![]() 时,
时,![]() 是
是![]() 的一次函数;当
的一次函数;当![]() 达到
达到![]() (尾/立方米)时,因缺氧等原因,
(尾/立方米)时,因缺氧等原因,![]() 的值为
的值为![]() (千克/年).
(千克/年).
(1)当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
(2)当养殖密度![]() 为多大时,鱼的年生长量(单位:千克/立方米)
为多大时,鱼的年生长量(单位:千克/立方米)![]() 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业想通过做广告来提高销售额,经预测可知本企业产品的广告费x(单位:百万元)与销售额y(单位:百万元)之间有如下对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
由表中的数据得线性回归方程为 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =6.5,由此预测当广告费为7百万元时,销售额为万元.
=6.5,由此预测当广告费为7百万元时,销售额为万元.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=ax+![]() (a>1),
(a>1),
(1)判断函数f(x)在(-1,+∞)上的单调性,并证明你的判断;
(2)若a=3,求方程f(x)=0的正根(精确到0.1).
查看答案和解析>>
科目: 来源: 题型:
【题目】设等差数列{an}满足(1﹣a1008)5+2016(1﹣a1008)=1,(1﹣a1009)5+2016(1﹣a1009)=﹣1,数列{an}的前n项和记为Sn , 则( )
A.S2016=2016,a1008>a1009
B.S2016=﹣2016,a1008>a1009
C.S2016=2016,a1008<a1009
D.S2016=﹣2016,a1008<a1009
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com