
科目: 来源: 题型:
【题目】已知函数f(x)=sin2x﹣ ![]() sinxcosx+
sinxcosx+ ![]() ,g(x)=mcos(x+
,g(x)=mcos(x+ ![]() )﹣m+2
)﹣m+2
(1)若对任意的x1 , x2∈[0,π],均有f(x1)≥g(x2),求m的取值范围;
(2)若对任意的x∈[0,π],均有f(x)≥g(x),求m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=sin(ωx﹣ ![]() )+sin(ωx﹣
)+sin(ωx﹣ ![]() ),其中0<ω<3,已知f(
),其中0<ω<3,已知f( ![]() )=0.
)=0.
(Ⅰ)求ω;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移 ![]() 个单位,得到函数y=g(x)的图象,求g(x)在[﹣
个单位,得到函数y=g(x)的图象,求g(x)在[﹣ ![]() ,
, ![]() ]上的最小值.
]上的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在![]() 年初的时候,国家政府工作报告明确提出,
年初的时候,国家政府工作报告明确提出, ![]() 年要坚决打好蓝天保卫战,加快解决燃煤污染问题,全面实施散煤综合治理.实施煤改电工程后,某县城的近六个月的月用煤量逐渐减少,
年要坚决打好蓝天保卫战,加快解决燃煤污染问题,全面实施散煤综合治理.实施煤改电工程后,某县城的近六个月的月用煤量逐渐减少, ![]() 月至
月至![]() 月的用煤量如下表所示:
月的用煤量如下表所示:
月份 |
|
|
|
|
|
|
用煤量 |
|
|
|
|
|
|
(1)由于某些原因, ![]() 中一个数据丢失,但根据
中一个数据丢失,但根据![]() 至
至![]() 月份的数据得出
月份的数据得出![]() 样本平均值是
样本平均值是![]() ,求出丢失的数据;
,求出丢失的数据;
(2)请根据![]() 至
至![]() 月份的数据,求出
月份的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)现在用(2)中得到的线性回归方程中得到的估计数据与![]() 月
月![]() 月的实际数据的误差来判断该地区的改造项目是否达到预期,若误差均不超过
月的实际数据的误差来判断该地区的改造项目是否达到预期,若误差均不超过![]() ,则认为该地区的改造已经达到预期,否则认为改造未达预期,请判断该地区的煤改电项目是否达预期?
,则认为该地区的改造已经达到预期,否则认为改造未达预期,请判断该地区的煤改电项目是否达预期?
(参考公式:线性回归方程![]() ,其中
,其中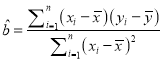
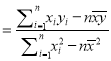 )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,按其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图中的信息,回答下列问题: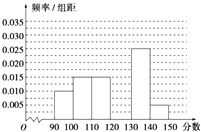
(Ⅰ)补全频率分布直方图;
(Ⅱ)估计本次考试的数学平均成绩(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)用分层抽样的方法在分数段为[110,130)的学生成绩中抽取一个容量为6的样本,再从这6个样本中任取2人成绩,求至多有1人成绩在分数段[120,130)内的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在![]() 年初的时候,国家政府工作报告明确提出,
年初的时候,国家政府工作报告明确提出, ![]() 年要坚决打好蓝天保卫战,加快解决燃煤污染问题,全面实施散煤综合治理.实施煤改电工程后,某县城的近六个月的月用煤量逐渐减少,
年要坚决打好蓝天保卫战,加快解决燃煤污染问题,全面实施散煤综合治理.实施煤改电工程后,某县城的近六个月的月用煤量逐渐减少, ![]() 月至
月至![]() 月的用煤量如下表所示:
月的用煤量如下表所示:
月份 |
|
|
|
|
|
|
用煤量 |
|
|
|
|
|
|
(1)由于某些原因, ![]() 中一个数据丢失,但根据
中一个数据丢失,但根据![]() 至
至![]() 月份的数据得出
月份的数据得出![]() 样本平均值是
样本平均值是![]() ,求出丢失的数据;
,求出丢失的数据;
(2)请根据![]() 至
至![]() 月份的数据,求出
月份的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)现在用(2)中得到的线性回归方程中得到的估计数据与![]() 月
月![]() 月的实际数据的误差来判断该地区的改造项目是否达到预期,若误差均不超过
月的实际数据的误差来判断该地区的改造项目是否达到预期,若误差均不超过![]() ,则认为该地区的改造已经达到预期,否则认为改造未达预期,请判断该地区的煤改电项目是否达预期?
,则认为该地区的改造已经达到预期,否则认为改造未达预期,请判断该地区的煤改电项目是否达预期?
(参考公式:线性回归方程![]() ,其中
,其中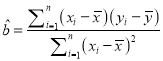
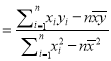 )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知以点A(﹣1,2)为圆心的圆与直线m:x+2y+7=0相切,过点B(﹣2,0)的动直线l与圆A相交于M、N两点
(1)求圆A的方程.
(2)当|MN|=2 ![]() 时,求直线l方程.
时,求直线l方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地区某中草药材的销售量与年份有关,下表是近五年的部分统计数据:
年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
销售量(吨) | 114 | 115 | 116 | 116 | 114 |
(1)利用所给数据求年销售量![]() 与年份
与年份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)利用(1)中所求出的直线方程预测该地2018年的中草药的销售量.
参考公式: 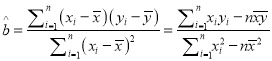 ,
, ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=Acos2(ωx+φ)+1(A>0,ω>0)的最大值为3,f(x)的图象在y轴上的截距为2,其相邻两对称轴间的距离为1,则f(1)+f(2)+f(3)+…+f(100)=( )
A.0
B.100
C.150
D.200
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com