
����Ŀ����![]() �����ʱ������������������ȷ�����
�����ʱ������������������ȷ����� ![]() ��Ҫ���������챣��ս���ӿ���ȼú��Ⱦ���⣬ȫ��ʵʩɢú�ۺ�����.ʵʩú�ĵ繤�̺�ij�سǵĽ������µ�����ú�����٣�
��Ҫ���������챣��ս���ӿ���ȼú��Ⱦ���⣬ȫ��ʵʩɢú�ۺ�����.ʵʩú�ĵ繤�̺�ij�سǵĽ������µ�����ú�����٣� ![]() ����
����![]() �µ���ú�����±���ʾ��
�µ���ú�����±���ʾ��
�·� |
|
|
|
|
|
|
��ú�� |
|
|
|
|
|
|
��1������ijЩԭ�� ![]() ��һ�����ݶ�ʧ��������
��һ�����ݶ�ʧ��������![]() ��
��![]() �·ݵ����ݵó�
�·ݵ����ݵó�![]() ����ƽ��ֵ��
����ƽ��ֵ��![]() �������ʧ�����ݣ�
�������ʧ�����ݣ�
��2�������![]() ��
��![]() �·ݵ����ݣ����
�·ݵ����ݣ����![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ��
��
��3�������ã�2���еõ������Իع鷽���еõ��Ĺ���������![]() ��
��![]() �µ�ʵ�����ݵ�������жϸõ����ĸ�����Ŀ�Ƿ�ﵽԤ�ڣ�������������
�µ�ʵ�����ݵ�������жϸõ����ĸ�����Ŀ�Ƿ�ﵽԤ�ڣ�������������![]() ������Ϊ�õ����ĸ����Ѿ��ﵽԤ�ڣ�������Ϊ����δ��Ԥ�ڣ����жϸõ�����ú�ĵ���Ŀ�Ƿ��Ԥ�ڣ�
������Ϊ�õ����ĸ����Ѿ��ﵽԤ�ڣ�������Ϊ����δ��Ԥ�ڣ����жϸõ�����ú�ĵ���Ŀ�Ƿ��Ԥ�ڣ�
���ο���ʽ�����Իع鷽��![]() ������
������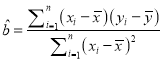
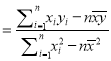 ��
��
���𰸡���1��4��2��![]() ��3���õ�����ú�ĵ���Ŀ�Ѿ��ﵽԤ��
��3���õ�����ú�ĵ���Ŀ�Ѿ��ﵽԤ��
�������������������1������ƽ�������㹫ʽ��![]() ����ö�ʧ�����ݣ���2�����ݹ�ʽ��
����ö�ʧ�����ݣ���2�����ݹ�ʽ��![]() ���ٸ���
���ٸ���![]() ��
��![]() ����3���������Իع鷽����������ݣ�����ʵ�����ݱȽ���ȷ������.
����3���������Իع鷽����������ݣ�����ʵ�����ݱȽ���ȷ������.
����������⣺��1���趪ʧ������Ϊ![]() ����
����![]()
��![]() ������ʧ��������
������ʧ��������![]() .
.
��2�����������![]() ��
��
�ɹ�ʽ���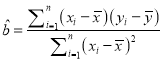
![]()
![]()
����![]() ����
����![]() �����Իع鷽��Ϊ
�����Իع鷽��Ϊ![]()
��3����![]() ʱ��
ʱ�� ![]() ��
�� ![]()
ͬ������![]() ʱ��
ʱ�� ![]() ��
�� ![]()
���ԣ��õ�����ú�ĵ���Ŀ�Ѿ��ﵽԤ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c�ֱ�Ϊ��ABC�����ڽ�A��B��C�ĶԱߣ�ccosA+ ![]() csinA��b��a=0��
csinA��b��a=0��
������C��
������c=1�����ABC����������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ��Բ��Ϊ
��Բ��Ϊ![]() ���ҽ�
���ҽ�![]() �����õ��ҳ�Ϊ
�����õ��ҳ�Ϊ![]() .
.
��1����Բ![]() �ķ��̣�
�ķ��̣�
��2����Բ![]() ��
��![]() ��������Ľ���Ϊ
��������Ľ���Ϊ![]() ����
����![]() �ֱ���б��Ϊ
�ֱ���б��Ϊ![]() ������ֱ�߽�Բ
������ֱ�߽�Բ![]() ��
��![]() ���㣬��
���㣬��![]() ����֤��ֱ��
����֤��ֱ��![]() ���һ���㣬������ö�������.
���һ���㣬������ö�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧΪ���˽��У��һ�꼶ѧ������ѧ�ɼ����Ӹ�һ�꼶���п��Գɼ��г��100��ѧ���ijɼ����ɳɼ��õ����µ�Ƶ�ʷֲ�ֱ��ͼ.
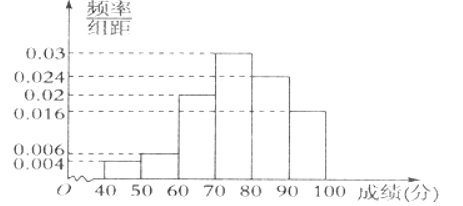
��������Ƶ�ʷֲ�ֱ��ͼ���ش��������⣺
��1������100��ѧ���ɼ��ļ����ʣ������ڵ���60��Ϊ����
��2���ԱȽ���100��ѧ����ƽ���ɼ�����λ���Ĵ�С.����ȷ��0.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ե�A����1��2��ΪԲ�ĵ�Բ��ֱ��m��x+2y+7=0���У�����B����2��0���Ķ�ֱ��l��ԲA�ཻ��M��N����
��1����ԲA�ķ��̣�
��2����|MN|=2 ![]() ʱ����ֱ��l���̣�
ʱ����ֱ��l���̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �Ƕ�����
�Ƕ�����![]() �ϵ��溯������
�ϵ��溯������![]() ����
����![]() ��
��![]() ʱ����
ʱ����![]() ����.
����.
�����ж�![]() ��
��![]() �ϵĵ����ԣ���֤����
�ϵĵ����ԣ���֤����
���ⲻ��ʽ![]() ��
��
������![]() �����е�
�����е�![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l��x��2y+2m��2=0��
��1������㣨2��3������ֱ��l��ֱ��ֱ�ߵķ��̣�
��2����ֱ��l������������Χ�ɵ������ε��������4����ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C��y2=2px��p��0�����ϵĵ�M��1��m�����佹��F�ľ���Ϊ2��
������C�ķ��̣��������߷��̣�
��II����֪A ��1����2�����Ƿ����ƽ����OA��OΪ����ԭ�㣩��ֱ��L��ʹ��ֱ��L��������C�й����㣬��ֱ��OA��L�ľ������ ![]() �������ڣ���ֱ��L�ķ��̣��������ڣ�˵�����ɣ�
�������ڣ���ֱ��L�ķ��̣��������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����粿�Ŷ�ij����![]() λ����2017��12�·��˾��õ��������ͳ�ƺ��˾��õ�����Ϊ
λ����2017��12�·��˾��õ��������ͳ�ƺ��˾��õ�����Ϊ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ���飬�����õ����µ�Ƶ�ʷֲ�ֱ��ͼ��������˵���������
���飬�����õ����µ�Ƶ�ʷֲ�ֱ��ͼ��������˵���������

A. ![]() �·��˾��õ�����������һ����
�·��˾��õ�����������һ����![]() ��
��
B. ![]() �·��˾��õ���������
�·��˾��õ���������![]() �ȵ���
�ȵ���![]() ��
��
C. ![]() �·��˾��õ���Ϊ
�·��˾��õ���Ϊ![]() ��
��
D. ����![]() λ��������ѡ
λ��������ѡ![]() λЭ���շѣ�ѡ���ľ����õ�����
λЭ���շѣ�ѡ���ľ����õ�����![]() һ��ĸ���Ϊ
һ��ĸ���Ϊ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com