
科目: 来源: 题型:
【题目】联合国教科文组织规定,每年的4月23日是“世界读书日”.某校研究生学习小组为了解本校学生的阅读情况,随机调查了本校400名学生在这一天的阅读时间![]() (单位:分钟),将时间数据分成5组:
(单位:分钟),将时间数据分成5组:![]() ,并整理得到如下频率分布直方图.
,并整理得到如下频率分布直方图.
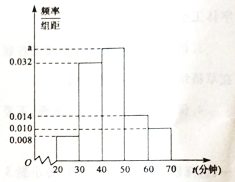
(1)求![]() 的值;
的值;
(2)试估计该学校所有学生在这一天的平均阅读时间;
(3)若用分层抽样的方法从这400名学生中抽取50人参加交流会,则在阅读时间为![]() 的两组中分别抽取多少人?
的两组中分别抽取多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】为了绿化城市,要在矩形区域ABCD内建一个矩形草坪,如图所示,另外,△AEF内部有一文物保护区不能占用,经测量AB=100 m,BC=80 m,AE=30 m,AF=20 m,应如何设计才能使草坪面积最大?

查看答案和解析>>
科目: 来源: 题型:
【题目】在一次趣味校园运动会的颁奖仪式上,高一、高二、高三代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就座,其中高二代表队有6人.

(1)求n的值;
(2)把在前排就座的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖.求a和b至少有一人上台抽奖的概率;
(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】直线l1 , l2分别过点A(3 ![]() ,2),B(
,2),B( ![]() ,6),它们分别绕点A,B旋转,但始终保持l1⊥l2 . 若l1与l2的交点为P,坐标原点为O,则线段OP长度的取值范围是( )
,6),它们分别绕点A,B旋转,但始终保持l1⊥l2 . 若l1与l2的交点为P,坐标原点为O,则线段OP长度的取值范围是( )
A.[3,9]
B.[3,6]
C.[6,9]
D.[9,+∞)
查看答案和解析>>
科目: 来源: 题型:
【题目】一名大学生尝试开家“网店”销售一种学习用品,经测算每售出1盒该产品可获利30元,未售出的商品每盒亏损10元.根据统计资料,得到该商品的月需求量的频率分布直方图如图所示,该同学为此购进180盒该产品,以x(单位:盒,100≤x≤200)表示一个月内的市场需求量,y(单位:元)表示一个月内经销该产品的利润.
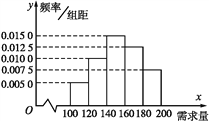
(1)根据直方图估计这个月内市场需求量x的平均数;
(2)将y表示为x的函数;
(3)根据直方图估计这个月利润不少于3 800元的概率(用频率近似概率).
查看答案和解析>>
科目: 来源: 题型:
【题目】把一枚质地均匀的骰子投掷两次,记第一次出现的点数为a,第二次出现的点数为b.已知方程组![]()
(1)求方程组只有一个解的概率;
(2)若方程组每个解对应平面直角坐标系中的点P(x,y),求点P落在第四象限的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】过三点A(﹣3,2),B(3,﹣6),C(0,3)的圆的方程为( )
A.x2+y2+4y﹣21=0
B.x2+y2﹣4y﹣21=0
C.x2+y2+4y﹣96=0
D.x2+y2﹣4y﹣96=0
查看答案和解析>>
科目: 来源: 题型:
【题目】用“斜二测”画法画出△ABC(A为坐标原点,AB在x轴上)的直观图为△A′B′C′,则△A′B′C′的面积与△ABC的面积的比为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线l:y=kx+1(k≠0)与椭圆3x2+y2=a相交于A、B两个不同的点,记l与y轴的交点为C.
(Ⅰ)若k=1,且|AB|= ![]() ,求实数a的值;
,求实数a的值;
(Ⅱ)若 ![]() =2
=2 ![]() ,求△AOB面积的最大值,及此时椭圆的方程.
,求△AOB面积的最大值,及此时椭圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com